Arduino Robot

" The Arduino Robot is the first robotics platform officially supported by Arduino.cc. It arrives fully assembled and nearly ready to run with no soldering required. Just plug in the color LCD screen, charge up the batteries (included), launch the Arduino IDE and upload the example code over the USB cable. The robot comes with a number of integrated inputs; two potentiometers, five buttons, a digital compass, five floor sensors, and an SD card reader. It also has a speaker, two motors, and a color screen as outputs, and plenty of prototyping space and TinkerKit connectors for expansion"
http://blog.makezine.com/2013/05/28/now-available-in-the-maker-shed-the-new-arduino-robot/

Linothorax

Da Wikipedia
"The linothorax is a modern term conventionally used to describe a type of upper body armor used by the Ancient Greeks, as well as other civilizations, from the Mycenaean Period through the Hellenistic Period. It is based on the Greek λινοθώραξ (in Homer λινοθώρηξ), which strictly is an adjective meaning "wearing a breastplate of linen" (and is not a noun meaning "linen armor" as often stated); the "linothorax" was made of linen, while a "thorax" was made of metal. The earliest attested account of a "linothorax" used for battle is recorded in Book 2 of Homer's Iliad (2.529 and 2.830). It is worn by Ajax the Lesser and is described in brief. Homer, composing long before the great armies of Athens, Thebes, Sparta or Alexander the Great, surely understood what the armor was. But the extent to which it was used can not be fully determined. An educated guess can be made, however, based on its use by Alexander the Great, and its mention by other sources such as Herodotus (2.182, 3.47, 7.63), Livy (4.19.2–20.7) and Strabo (Geography, 3.3.6, 13.1.10), and many others. The linothorax appears to have been used in place of the bronze 'bell cuirass' as the popular choice of armour for Greek hoplites, starting perhaps around the late seventh century and early sixth century B.C. Its high point, if vase paintings, sculptural reliefs and artistic depictions are to be believed, corresponds with the time of the Persian Wars. By the time of the Peloponnesian War it was still used, and continued to seemingly flourish well into the Hellenistic Period."

After 150 years, the Stirling motor lives

The Sydney Morning Herald, 26 May, 1975

Ford Torino Stirling Special

Ford Torino Stirling Special

da

Modello matematico di motore Stirling accoppiato ad un generatore
elettrico lineare,  Michele Favaron

http://tesi.cab.unipd.it/37661/1/Modello_matematico_di_motore_Stirling_accoppiato_ad_un_generatore_lineare.pdf

Motore di Stirling fatto in casa

Su YouTube cercando "motore stirling fatto in casa" trovate diversi progetti per crearvi il vostro "motore".

A liquid telescope

http://en.wikipedia.org/wiki/Liquid_mirror_telescope

Liquid mirror telescopes are telescopes with mirrors made with a reflective liquid. The most common liquid used is mercury. The container for the liquid is rotating so that the liquid assumes a paraboloidal shape. A paraboloidal shape is precisely the shape needed for the primary mirror of a telescope. The rotating liquid assumes the paraboloidal shape regardless of the container's shape.  Liquid mirrors can be a low cost alternative to conventional large telescopes. Compared to a solid glass mirror that must be cast, ground, and polished, a rotating liquid metal mirror is much less expensive to manufacture.

"Isaac Newton noted that the free surface of a rotating liquid forms a circular paraboloid and can therefore be used as a telescope, but he could not actually build one because he had no way to stabilize the speed of rotation[citation needed] (the electric motor did not exist yet). The concept was further developed by Ernesto Capocci of the Naples Observatory (1850), but it was not until 1872 that Henry Skey of Dunedin, New Zealand constructed the first working laboratory liquid mirror telescope."

"Another difficulty is that a telescope with a liquid metal mirror can only be used in zenith telescopes that look straight up at the zenith, so it is not suitable for investigations where the telescope must remain pointing at the same location of space ... Currently, the mercury mirror of the Large Zenith Telescope in Canada is the largest liquid metal mirror in operation. It has a diameter of six meters, and rotates at a rate of about 8.5 revolutions per minute."

Variazione entropia

Un esercizio del prof. Mussino che propone un semplice calcolo della variazione d'entropia.

Un sistema termodinamico formato ...

Sempre un esame Prfo.Mussino

Una mole di gas ideale ...

Problema esame Prof. Mussino

n.5 punto di massa ....

Problema d'esame del Prof. Mussino

Un punto di massa m viene lasciato dalla posizione A con velocità v_o= 10 m/s lungo un piano inclinato con angolo θ = 30°; h vale 0.26 m, il coefficiente di attrito dinamico è μ=0.1. Calcolare quanto tempo impiega il punto per arrivare nella posizione B e quanto dovrebbe valere μ per far sì che il punto arrivi in B con velocità nulla.

Un gas ideale biatomico ...

Il ciclo di Carnot

Al link
http://books.google.it/books/about/R%C3%A9flexions_sur_la_puissance_motrice_du.html?id=YcY9AAAAMAAJ&redir_esc=y
il libro di Carnot dove descrve il ciclo.

Alcune pagine di una versione inglese del 1897

Nicolas Léonard Sadi Carnot

http://en.wikipedia.org/wiki/Nicolas_L%C3%A9onard_Sadi_Carnot

Carnot's Reflections on the Motive Power of Fire 

When Carnot began working on his book, steam engines had achieved widely recognized economic and industrial importance, but there had been no real scientific study of them. Newcomen had invented the first piston-operated steam engine over a century before, in 1712; some 50 years after that, James Watt made his celebrated improvements, which were responsible for greatly increasing the efficiency and practicality of steam engines. Compound engines (engines with more than one stage of expansion) had already been invented, and there was even a crude form of internal-combustion engine, with which Carnot was familiar and which he described in some detail in his book. Although there existed some intuitive understanding of the workings of engines, scientific theory for their operation was almost nonexistent. In 1824 the principle of conservation of energy was still poorly developed and controversial, and an exact formulation of the first law of thermodynamicswas still more than a decade away; the mechanical equivalence of heat would not be formulated for another two decades. The prevalent theory of heat was the caloric theory, which regarded heat as a sort of weightless and invisible fluid that flowed when out of equilibrium.

Engineers in Carnot's time had tried, by means such as highly pressurized steam and the use of fluids, to improve the efficiency of engines. In these early stages of engine development, the efficiency of a typical engine — the useful work it was able to do when a given quantity of fuelwas burned — was only 3%.

The Carnot Cycle 

Carnot sought to answer two questions about the operation of heat engines: "Is the work available from a heat source potentially unbounded?" and "Can heat engines in principle be improved by replacing the steam with some other working fluid or gas?" He attempted to answer these in a memoir, published as a popular work in 1824 when he was only 28 years old. It was entitled Réflexions sur la Puissance Motrice du Feu ("Reflections on the Motive Power of Fire"). The book was plainly intended to cover a rather wide range of topics about heat engines in a rather popular fashion; equations were kept to a minimum and called for little more than simple algebra and arithmetic, except occasionally in the footnotes, where he indulged in a few arguments involving some calculus. He discussed the relative merits of air and steam as working fluids, the merits of various aspects of steam engine design, and even included some ideas of his own regarding possible improvements of the practical nature. The most important part of the book was devoted to an abstract presentation of an idealized engine that could be used to understand and clarify the fundamental principles that are generally applied to all heat engines, independent of their design.

Perhaps the most important contribution Carnot made to thermodynamics was his abstraction of the essential features of the steam engine, as they were known in his day, into a more general and idealized heat engine. This resulted in a model thermodynamic system upon which exact calculations could be made, and avoided the complications introduced by many of the crude features of the contemporary steam engine. By idealizing the engine, he could arrive at clear and indisputable answers to his original two questions.

He showed that the efficiency of this idealized engine is a function only of the two temperatures of the reservoirs between which it operates. He did not, however, give the exact form of the function, which was later shown to be ^{(T₁−T₂)}⁄_T1, where T₁ is the absolute temperature of the hotter reservoir. (Note: This equation probably came from Kelvin.) No thermal engine operating any other cycle can be more efficient, given the same operating temperatures.

The Carnot cycle is the most efficient possible engine, not only because of the (trivial) absence of friction and other incidental wasteful processes; the main reason is that it assumes no conduction of heat between parts of the engine at different temperatures. Carnot knew that the conduction of heat between bodies at different temperatures is a wasteful and irreversible process, which must be eliminated if the heat engine is to achieve maximum efficiency.

Regarding the second point, he also was quite certain that the maximum efficiency attainable did not depend upon the exact nature of theworking fluid. He stated this for emphasis as a general proposition: "The motive power of heat is independent of the agents employed to realize it; its quantity is fixed solely by the temperatures of the bodies between which the transfer of caloric takes place." For his "motive power of heat", we would today say "the efficiency of a reversible heat engine," and rather than "transfer of caloric" we would say "the reversible transfer of heat." He knew intuitively that his engine would have the maximum efficiency, but was unable to state what that efficiency would be.

He concluded:

The production of motive power is therefore due in steam engines not to actual consumption of caloric but to its transportation from a warm body to a cold body.

—Carnot 1960, p. 7

and

In the fall of caloric, motive power evidently increases with the difference of temperature between the warm and cold bodies, but we do not know whether it is proportional to this difference.

—Carnot 1960, p. 15

The Second Law of Thermodynamics 

In Carnot's idealized model, the caloric heat converted into work could be recovered by reversing the motion of the cycle, a concept subsequently known as thermodynamic reversibility. Nevertheless, Carnot further postulated that some caloric is lost and not converted into mechanical work. Hence, a real heat engine could not realize the Carnot cycle's reversibility and would consequently be less efficient.

Though formulated in terms of caloric, rather than entropy, this was an early rendition of the second law of thermodynamics.

Reception and later life 

Carnot’s book received very little attention from his contemporaries. The only reference to it within a few years after its publication was in a review in the periodical Revue Encyclopédique, which was a journal that covered a wide range of topics in literature. The impact of the work had only become apparent once it was modernized by Émile Clapeyron in 1834 and then further elaborated upon by Clausius and Kelvin, who together derived from it the concept of entropy and the second law of thermodymics.

Adiabatica

Cosmic Microwave Background Radiation
http://www.nicadd.niu.edu/~bterzic/PHYS652/Lecture_19.pdf  by Balša Terzić  
"The CMB radiation is a prediction of Big Bang theory. According to the Big Bang theory, the
early Universe was made up of a hot plasma of photons, electrons and baryons. The photons were
constantly interacting with the plasma through Thomson scattering. As the Universe expanded,
adiabatic cooling caused the plasma to cool until it became favorable for electrons to combine
with protons and form hydrogen atoms. This happened at around 3,000 K or when the Universe
was approximately 380,000 years old (z ≈ 1100). At this point, the photons scattered off the
now neutral atoms and began to travel freely through space. This process is called recombination
or decoupling (referring to electrons combining with nuclei and to the decoupling of matter and
radiation respectively). The photons have continued cooling ever since; they have now reached 2.725 K and their temperature will continue to drop as long as the Universe continues expanding. Accordingly,
the radiation from the sky that we measure today comes from a spherical surface, called the surface of last scattering. This represents the collection of points in space (currently around 46 billion light years from the Earth) at which the decoupling event happened long enough ago (less than 400,000 years after the Big Bang, 13.7 billion years ago) that the light from that part of space is just reaching observers."

Sul LAVORO in termodinamica

Lavoro in termodinamica 

In termodinamica, il lavoro viene scomposto per comodità in due contributi: un contributo relativo alla variazione di volume (lavoro di volume) e un contributo indipendente dalla variazione di volume (lavoro isocoro).

Lavoro di volume

In termodinamica un gas esercita una pressione P interna sulle pareti del recipiente in cui è contenuto. Se una di queste pareti (di area A) è mobile e si sposta di una quantità infinitesima dl sotto l'azione di questa pressione, allora il lavoro infinitesimo compiuto dal gas è dato da:

.

dove dV = A dl è la variazione del volume corrispondente. Questo è vero se la trasformazione è reversibile, infatti solo se il sistema è in equilibrio termodinamico è possibile conoscere il valore della pressione P interna al contenitore. La notazione  è usata per indicare che il lavoro in fisica non è una funzione di stato, ed invece dipende dalla particolare trasformazione eseguita sul sistema. Se il sistema termodinamico subisce una trasformazione dove non si consoce p, quindi in una tarsformazione irreversibile, il lavoro  lo possiamo determinare sfruttando il primo principio della termodinamcia, conoscendo calo scambiato e variazione d'energia interna. Possiamo ancora quantificare il lavoro fatto dal gas o dal sistema comeì:

,

lavoro fatto contro la pressione esterna , se ammettiamo di consocere la pressione esterna.

La termodinamica non è fatta solo di sistemi P,V,T (fluidi) e quindi ci può essere un lavoro "isocoro"

Lavoro isocoro 

Sotto il termine di lavoro isocoro si annoverano tutti i tipi di lavoro che non si riflettono in una variazione di volume, ad esempio: il lavoro elettrico. 

Lavoro elettrico: In un circuito elettrico il lavoro infinitesimo compiuto dalla batteria che genera la differenza di potenziale E per far circolare una corrente elettrica I per un tempo infinitesimo dt è data da , il segno di tale lavoro sarà positivo o negativo a seconda che rispettivamente la pila eroghi o assorba corrente. Il valore del lavoro elettrico scambiato tra il tempo t₀ e il tempo t₁ si può ottenere integrando l'equazione precedente, dalla quale si ottiene:

nel caso in cui la differenza di potenziale E rimanga costante durante l'intervallo di tempo considerato, si può scrivere:

essendo:

• L il lavoro elettrico (in joule);
• E la differenza di potenziale elettrico (in volt);
• I l'intensità di corrente elettrica in (in ampere);
• t il tempo (in secondi);
• Q_el la quantità di carica elettrica circolata durante l'intervallo di tempo considerato (in coulomb).

The spinning top

Rotate vs revolve

Rotate versus revolve, from http://www.worldwidewords.org/nl/uifj.htm
by MICHAEL QUINION

Q From Brian Miller, Australia: A loosely organised group of eccentric friends and wine lovers meets each week. The question arose, does a lazy Susan revolve or rotate? What about the plates on it?

A That’s an interesting question, which lacks a simple answer. If anybody’s not sure about a lazy Susan, by the way, it’s a device on a table which turns to give easy access to plates and condiments.

... The two words are used so interchangeably in the sense of spinning round that for most purposes they’re synonyms and they’re treated as such in thesauruses. To take an example, does a wheel rotate or revolve? Most people would say it can do either.

If you’re arguing from etymology (always risky), it can only rotate, since that term is from the Latin verb rotare, to turn in a circle, whose root is rota, a wheel. But you might argue that it revolves, because that verb is from the Latin volvere, to roll (in this case, the re- prefix implies repetition of the action) and a wheeled vehicle certainly does roll along.

Strictly speaking, there is a difference, which is most noticeable in the terminology of astronomers. For them, the earth rotates every 24 hours but takes a year to revolve around the sun. The rule about which verb to use is based on the position of the axis of rotation. If the body turns on an axis within itself it rotates but if the axis is outside it revolves. Following this definition, a wheel can only rotate (hooray for etymology).

The strict answer to the question, therefore, is that the lazy Susan rotates. However, because the plates on it orbit or circle around an axis outside themselves, they revolve. Do not insist on this careful distinction during the later stages of a dinner party or the lazy Susan may become a spinning projectile aimed at you.

As I say, the rule is rarely observed outside science and the two words have been hopelessly muddled for centuries. A revolving door actually rotates; a rotating shaft makes revolutions. You might argue that a revolver ought to be a rotator but it depends whether you are thinking of the cartridges or the cylinder that holds them.

La trottola

Da "Semplicemente fisica. Fraintendimenti, bugie, buchi neri nell'apprendimento scolastico della fisica", di  Giovanni Tonzig, Maggioli Editore, 2010 - 227 pagine

Space Oddity

Assembly line

"The assembly line was invented 100 years ago. It’s time to invent the disassembly line", Steven Cherry is telling at

http://spectrum.ieee.org/podcast/at-work/innovation/the-future-of-the-assembly-line

in a conversation with David Nye,  professor of American history at the University of Southern Denmark.

Deep Space Beacon

Pulsed gamma rays from the Vela pulsar  from photons detected by Fermi's Large Area Telescope. The Vela pulsar is the brightest persistent source of gamma rays in the sky. The bluer colour in the latter part of the pulse indicates the presence of gamma rays with energies exceeding a billion electron volts (1 GeV). For comparison, visible light has energies between two and three electron volts. Red indicates gamma rays with energies less than 300 million electron volts (MeV); green, gamma rays between 300 MeV and 1 GeV; and blue shows gamma rays greater than 1 GeV. The image frame is 30 degrees across. The background, which shows diffuse gamma-ray emission from the Milky Way, is about 15 times brighter here than it actually is.
Source Goddard Space Flight Center
Author Roger Romani (Stanford University) (Lead), Lucas Guillemot (CENBG), Francis Reddy (SPSYS)

n.23 - Joe e Moe

Un cuneo di massa M è in quiete su una superficie orizzontale priva di attrito. Un blocco di massa m è posto sul cuneo. Non c'è attrito tra il blocco e il cuneo. Il sistema è lasciato libero da fermo. Calcolate: a) l'accelerazione del cuneo, 2) le componenti orizzontale e verticale dell'accelerazione del blocco, e verificate il limite M che tende a infinito.

A wedge with mass M rests on a frictionless horizontal tabletop. A block with mass m is placed on the wedge. There is no friction between the block and the wedge. The system is released from rest. Calculate 1) the acceleration of the wedge, 2) the horizontal and vertical components of the acceleration of the block, check the limit when M  --- > infinite. 

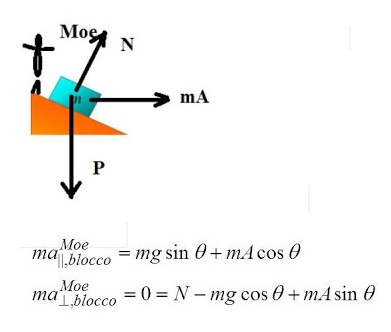
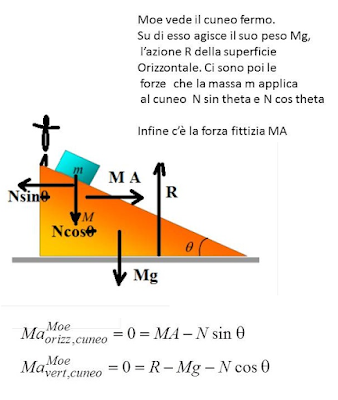
Risolviamo il problema con Joe e Moe, ossia col moto relativo.

Consideriamo due osservatori: Joe è fermo sul piano orizzontale e Moe è fermo sul cuneo.

Joe vede che il blocco m si muove sul cuneo  scendendo verso destra  e che il cuneo si muove verso sinistra  con una accelerazione A. Moe, che è sul cuneo, non vede il cuneo muoversi, ma vede la massa m  che si muove soggetta al peso, alla normale N del cuneo e alla forza  fittizia mA verso destra.

Scriviamo l’equazione per l’accelerazione  del blocco m, PARALLELA al piano inclinato,  che fornisce  l’accelerazione lungo il piano inclinato  vista da Moe, e poi scriviamo l’equazione  d’equilibrio lungo la PERPENDICOLARE al piano inclinato:

GAMMA RAYS and Gamma-Ray Burst

Gamma rays have the smallest wavelengths and the most energy of any wave in the electromagnetic spectrum. ... http://missionscience.nasa.gov/ems/12_gammarays.html
Gamma-ray bursts (GRBs) are flashes of gamma rays associated with extremely energetic explosions that have been observed in distant galaxies. They are the brightest electromagnetic events known to occur in the universe.[1] Bursts can last from ten milliseconds to several minutes. The initial burst is usually followed by a longer-lived "afterglow" emitted at longer wavelengths (X-ray, ultraviolet, optical, infrared, microwave and radio).[2] http://en.wikipedia.org/wiki/Gamma-ray_burst...
On April 27, 2013, NASA's Fermi and Swift satellites detected a strong signal from the brightest gamma-ray burst in decades. Because this was relatively close, it was thousands of times brighter than the typical gamma-ray bursts that are seen by Swift every few days. Scientists are now scrambling to learn more....
http://edition.cnn.com/2013/05/06/opinion/urry-gamma-ray-burst/index.html?sr=sharebar_twitter

Cilindro e oscillazioni

Baricole

Da "Storia e leggenda del vetro" di Paolo Mazzoldi
http://www.edscuola.it/archivio/lre/storia_del_vetro.pdf

rendimento

n.19 - cubetto ghiaccio

Un cubetto di ghiaccio scende lungo uno scivolo, posto in un piano verticale, privo di attrito.

Esce dallo scivolo con un angolo di 40°. Dopo l'urto con la parete, la componente orizzontale della velicità si riduce della metà. Conoscendo l'altezza dello scivolo h e la massa (10g) del cubetto, trovate l'impulso del cubetto sulla parete.

Il problema non è certo difficile, ma si deve far attenzione al fatto che la quantità di moto è un vettore, e di ciò si deve tener conto nel calcolo dell'impuslo, che è pari alla variazione della quantità di moto.

Rendimento

n.16 - Esercizio elettrostatica

n.32 - Asta

n.34 - statica e altro

Solo la prima parte è stata presa come esercizio per un esame.

Sun reflection

Courtesy: NASA Apollo 8

View of Earth as photographed by the Apollo 8 astronauts on their return trip from the moon. The terminator crosses Australia. India is visible. The sun reflection is within the Indian Ocean.

Renaissance of Rome

In 1586 Domenico Fontana erected the obelisk in the Square of St. Peter's. Wiki: "This feat of engineering took the concerted effort of 900 men, 75 horses and countless pulleys and meters of rope. He gives a detailed account of it in Della transportatione dell'obelisco Vaticano e delle fabriche di Sisto V (Rome, 1590) [1] [2]. The astronomer Ignazio Danti is known to have assisted Fontana in this work. Fontana also used his knowledge of statics, which aroused universal astonishment at the time, in the erection of three other ancient obelisks on the Piazza del Popolo, Piazza di S. Maria Maggiore, and Piazza di S. Giovanni in Laterano."

Nanocanyons in Multilayer Laue Lenses

Nanocanyons in Multilayer Laue Lenses

Brookhaven National Laboratory:  A scanning electron microscope captured this from the bottom of a trench carved by reactive ion etching. 

Dancing Men in Renaissance Painting May Be Native Americans

Dancing Men in Renaissance Painting May Be Native Americans

Friday, May 03, 2013
VATICAN CITY—While restoring a fresco painted in 1494 by Pinturicchio on the walls of the Vatican’s Borgia Apartments, Maria Pustka found small images of dancing men that may be the first Western depictions of Native Americans. “The Borgia Pope was interested in the New World, as were the great chancelleries of Europe. It is hard to believe that the papal court, especially under a Spanish pope, would have remained in the dark about what Columbus encountered,” wrote Antonio Paolucci, director of the Vatican Museums. That pope would eventually arbitrate the division of New World lands between Spain and Portugal.

The 'irreproducibility' problem

The 'irreproducibility'  AAAS
Interessante discussione sull'irriproducibilità di alcuni esperimenti.

A Year Without a Summer

The 'Year Without a Summer' AAAS
"In many parts of the country winter refuses to release its icy grip, and records are being broken for spring’s late arrival. Although we know that spring and summer will come eventually, we are still a far cry from rivaling the “Year Without a Summer.”  That year was 1816. It was near the end of the Little Ice Age, a period that began around 1350 AD. It was also in the middle of what became known as the Dalton Minimum, an unusual period of low solar activity named after English meteorologist John Dalton that lasted from 1790 to 1830...."

Teorema di Bernoulli

Primo Teorema di Koenig

Il I Teorema di Koenig riguarda il momento angolare di un sistema

Consideriamo un sistema di particelle in un riferimento inerziale. Scegliamo in questo riferimento il punto fisso O. Prendiamo i raggi vettore che vanno da O a ciascuna particella e il raggio vettore che individua la posizione del centro di massa CM. Indicando con i la i-esima particella, definiamo r'i e v'i come:

Il momento angolare del sistema, valutato rispetto al polo fisso, lo possiamo vedere come la somma di due termini: uno è il momento angolare L' con i vettori posizione r' e vettori velocità v' valutati rispetto al CM e l'altro è il momento della quantità di moto del sistema, momento valutato rispetto a O.

Se ho un sistema costituito da  un copro rigido, una parte del momento angolare viene dal moto del centro di massa, come se tutta la massa fosse concentrata in esso (ad esempio la rivoluzione del centro di massa della terra). L'altra parte viene dal moto relativo al centro di massa delle particelle (ad esempio la rotazione della terra su se stessa). 

II Equazione cardinale sistemi

Seconda equazione cardinale dei sistemi col calcolo rispetto a polo fisso.

Questa equazione riguarda l'evoluzione temporale del momento angolare di un sistema.
Si definisce come momento angolare di una particella di massa m e di velocità v il vettore:

definito tramite il prodotto vettoriale o prodotto esterno tra il vettore posizione r ed il vettore P=mv quantità di moto. Nella definizione del momento angolare abbiamo introdotto il vettore posizione: questo vettore è definito rispetto ad un punto scelto come polo O. Il polo lo consideriamo come un punto fisso nel riferimento inerziale scelto. Se si cambia il punto O cambia anche il vettore L. Infatti, se si cambio il polo in O’, la relazione che lega il nuovo momento angolare L’ calcolato rispetto al punto O' ed il momento angolare L rispetto ad O è la seguente:

Il momento di una forza è definito come:

che dipende dalla scelta del punto O come per il momento angolare. Nel calcolo, il polo deve essere lo stesso per il momento angolare e per il momento della forza. 

Calcoliamo la derivata rispetto al tempo del vettore L. Per la derivazione applichiamo la stessa regola già vista per la derivazione dei prodotti di funzioni:

che è la relazione che rappresenta il teorema del momento angolare per un punto materiale: la derivata temporale del momento angolare è uguale al momento della forza. Il termine vxmv è nullo essendo il prodotto esterno di due vettori paralleli. Il momento della forza può essere nullo se la forza è nulla oppure se i vettori r ed F sono paralleli (come ad esempio nel caso delle forze centrali, con il centro preso come polo):

Il momento angolare di un punto materiale rimane costante nel tempo (e cioè si conserva) se il momento delle forze è nullo.

Supponiamo di avere adesso un insieme di particelle di massa m_i e di vettori velocita’ v_i. La posizione di ciascuna particella rispetto al polo O sia il vettore r_i. Il momento angolare totale sarà:

L’indice i varia da 1 a N, numero totale delle particelle.

Enunciamo il teorema del momento angolare per un sistema di particelle. Se il punto O rispetto a cui calcoliamo il vettore posizione è fisso nel riferimento inerziale l'evoluzione nel tempo del momento angolare del sistema di punti è determinato dal momento delle forze esterne rispetto ad O, mentre le forze interne non portano alcun contributo.

Dato il momento totale delle forze esterne:

Quando si conserva il momento angolare? Quando il vettore t ^ext è nullo e questo capita quando il momento totale delle forze è nullo oppure quando non vi sono forze esterne che agiscono sul sistema stesso e cioè è il sistema è isolato.

Dimostriamo il teorema del momento angolare per un sistema di due particelle. Queste due particelle possono essere una coppia appartenente ad un sistema: la dimostrazione fatta per la coppia ovviamente può essere ripetuta per ciascuna coppia del sistema, e quindi estendere la dimostrazione a tutto il sistema.

Calcoliamo il momento totale delle forze che agiscono sulla particella i e sulla particella j:

dove i vettori F sono le forze esterne e i vettori f sono le forze interne.

Siccome le forze interne hanno la stessa retta d'azione e il modulo uguale ma verso opposto:

Il prodotto esterno è nullo perché fatto tra due vettori paralleli. Rimangono solo i momenti delle forze esterne al sistema.