Problema doppio piano inclinato

Problema dinamica e moto relativo

Sopra un piano orizzontale è poggiato un cubo di massa M, che può scorrere senza attrito sul piano orizzontale. Sopra il cubo è poggiato un altro cubetto di massa m a distanza d dalla faccia di sinistra del cubo più grande. All'istante iniziale, quando tutto è fermo, al cubo è applicata una forza F orizzontale. Questa forza è costante; dopo t il cubetto cade. Calcolare il coefficiente di attrito tra i due cubi. (Dati del problema M=50 kg, m=10 kg, d=50 cm, F=100 N, t=2 s)

Problema momento impulso

Una sbarra di lunghezza L=40 cm, di massa trascurabile, che è incernierata ad un estremo ad un perno fisso, può muoversi liberamente in un piano verticale. La sbarra ha attaccata all’altro estremo una massa m di 2.5 kg. La sbarra e la massa sono inizialmente ferme, con l’asta verticale e la massa in basso. La massa riceve un impulso e compie un quarto di giro. Determinare la velocità angolare che assume inizialmente la massa e l'impulso che viene applicato.

Problema dinamica

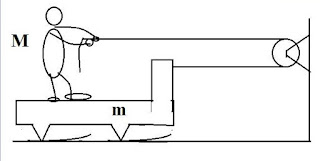
Una persona si trova su una pedana mobile. Tra la pedana ed il pavimento l’attrito è trascurabile. Tra la persona e la pedana c’è attrito statico. La persona tira la fune e nella fune si sviluppa una tensione T di 20 N. La massa M è di 60 kg, la pedana è di 20 kg. Trovate l’accelerazione di persona e pedana.

La persona non scivola sulla pedana. C'è l'attrito statico che crea la forza A orizzontale. Le due figure con le frecce colorate sono i diagrammi di corpo libero per la persona (M) e per la pedana (m).

Problema dinamica

Calcolare l’accelerazione del sistema fatto da una massa m e da una pedana M, come in figura. Il filo è inestensibile e privo di massa, così come la carrucola. La massa mobile è appoggiata alla parete verticale del carrello. Non vi sono attriti.

Problema dinamica

Una persona si trova su una pedana mobile. Tra la pedana ed il pavimento l’attrito è trascurabile. Tra la persona e la pedana c’è attrito statico. La persona tira la fune e nella fune si sviluppa una tensione T di 20 N. La massa M è di 60 kg, la pedana è di 20 kg. Trovate l’accelerazione di persona e pedana.

Pedana M:   M a = T  (verso destra);    M g = N  dove N è l'azione del pavimento

Massa m: ma = mg ─ T (verso il basso) 

La fune  è inestensibile, sommo  equazioni

Ma + ma = T + mg -T = mg

a = mg/(M+m)

Problema dinamica

Una ragazza di 60 kg sta in piedi su una piattaforma di alluminio di 15 kg per dipingere una casa. Una fune attaccata alla piattaforma e passante su una carrucola fissata al soffitto consente alla ragazza di sollevare se stessa e la piattaforma. (a) Per muoversi la ragazza imprime a se stessa e alla piattaforma un'accelerazione di 0,8 m/s². Con che forza deve tirare la corda? (b) Dopo 1 s la ragazza tira in modo da salire con la piattaforma con la velocità costante di 1 m/s. Che forza deve esercitare sulla corda?
[Ris. (a) 397 N; (b) 367 N.] Vedi anche https://physicstasks.eu/278/boy-on-a-pulley

m _r = 60 kg , m_p = 15 kg , m _tot = 75 kg , a = 0.8 m/s² , g = 9.8 m/s²

A) Sia F la forza applicata F dalla ragazza che tira la fune verso il basso. Sia T la tensione della fune.
Dobbiamo trovare la forza F. Sia la direzione verso l'alto quella positiva. Si ha
F = T (in modulo)

Sulla massa totale: T + F - m_tot g = m_r a 

2 F = m_r (a + g) da cui F = 397 N 

Dove la ragazza applica la forza, si ha in modulo F = T (azione e reazione). La forza F è verso il basso e la reazione è verso l'alto; così la corda agisce sulla ragazza verso l'alto.

B) a=0
F = T
T + F - m_r g = 0
2F = m_r g e quindi: F = 367 N

Problema dinamica

Fate il problema che trovate al link

https://physicstasks.eu/278/boy-on-a-pulley

n.10 - Massa e due molle

Esercizio esame prof. Alfredo Strigazzi

n.5 punto di massa ....

Problema d'esame del Prof. Mussino

Un punto di massa m viene lasciato dalla posizione A con velocità v_o= 10 m/s lungo un piano inclinato con angolo θ = 30°; h vale 0.26 m, il coefficiente di attrito dinamico è μ=0.1. Calcolare quanto tempo impiega il punto per arrivare nella posizione B e quanto dovrebbe valere μ per far sì che il punto arrivi in B con velocità nulla.

n.23 - Joe e Moe

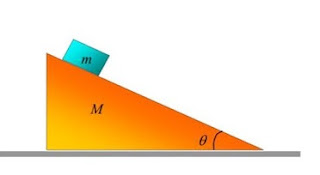
Un cuneo di massa M è in quiete su una superficie orizzontale priva di attrito. Un blocco di massa m è posto sul cuneo. Non c'è attrito tra il blocco e il cuneo. Il sistema è lasciato libero da fermo. Calcolate: a) l'accelerazione del cuneo, 2) le componenti orizzontale e verticale dell'accelerazione del blocco, e verificate il limite M che tende a infinito.

A wedge with mass M rests on a frictionless horizontal tabletop. A block with mass m is placed on the wedge. There is no friction between the block and the wedge. The system is released from rest. Calculate 1) the acceleration of the wedge, 2) the horizontal and vertical components of the acceleration of the block, check the limit when M  --- > infinite. 

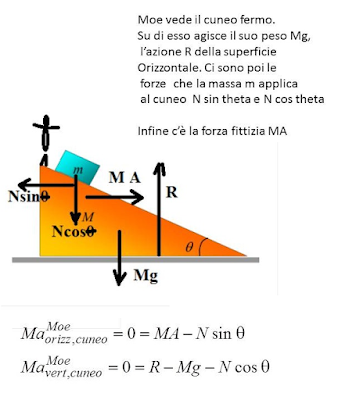
Risolviamo il problema con Joe e Moe, ossia col moto relativo.

Consideriamo due osservatori: Joe è fermo sul piano orizzontale e Moe è fermo sul cuneo.

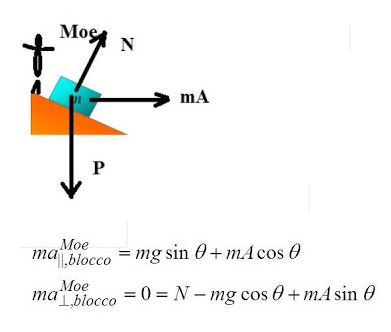
Joe vede che il blocco m si muove sul cuneo  scendendo verso destra  e che il cuneo si muove verso sinistra  con una accelerazione A. Moe, che è sul cuneo, non vede il cuneo muoversi, ma vede la massa m  che si muove soggetta al peso, alla normale N del cuneo e alla forza  fittizia mA verso destra.

Scriviamo l’equazione per l’accelerazione  del blocco m, PARALLELA al piano inclinato,  che fornisce  l’accelerazione lungo il piano inclinato  vista da Moe, e poi scriviamo l’equazione  d’equilibrio lungo la PERPENDICOLARE al piano inclinato:

n.19 - cubetto ghiaccio

Un cubetto di ghiaccio scende lungo uno scivolo, posto in un piano verticale, privo di attrito.

Esce dallo scivolo con un angolo di 40°. Dopo l'urto con la parete, la componente orizzontale della velicità si riduce della metà. Conoscendo l'altezza dello scivolo h e la massa (10g) del cubetto, trovate l'impulso del cubetto sulla parete.

Il problema non è certo difficile, ma si deve far attenzione al fatto che la quantità di moto è un vettore, e di ciò si deve tener conto nel calcolo dell'impuslo, che è pari alla variazione della quantità di moto.

n.3 - massa e pulegge

n.26 - il rotor

Il rotor del parco di divertimenti.