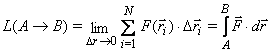Lavoro e teorema energia cinetica

Prima di discutere il lavoro come integrale lungo una linea del prodotto scalare di forza e spostamento infinitesimo, discutiamo un semplice problema unidimensionale che ci può mostrare in modo semplice il legame del lavoro con l'energia cinetica. Prendiamo una particella di massa m a cui sia applicata una forza F, costante in modulo direzione e verso. Sia x l'asse coincidente con la direzione della forza  su cui si muove, di conseguenza, la particella di massa m. Siccome la forza è costante anche l'accelerazione lo sarà:  

Abbiamo quindi visto con questo semplice calcolo unidimensionale che esiste una relazione tra la quantità  dimensionata come [forza∙spotamento] con la differenza di due grandezze che sono dimensionate [massa.velocità^2]. Siccome [forza]=[massa∙accelerazione]=[massa∙velocità/tempo], abbiamo che  [forza∙spostamento]=[massa∙(velocità/tempo)∙spostamento]=[msssa∙velocità∙spotamento/tempo]=[m∙velocità^2].

         

Se definiamo E_cin=1/2 mv² come l' energia cinetica allora l'equazione ci dice che la variazione dell'energia cinetica ΔE_cin=1/2 mv² − 1/2 mv_o² ossia la differenza tra l'energia cinetica finale e quella iniziale è uguale al prodotto di F∙per (x-x_o) che è il  lavoro compiuto dalla forza applicata alla particella. L'unità di misura del lavoro nel sistema internazionale è il  Joule ed è definito come il lavoro compiuto dalla forza di un Newton che agisce per un metro. Passiamo adesso ad affrontare la definizione di lavoro per uno spostamento generico.

Definiamo lavoro L compiuto da una forza F su una particella che subisce uno spostamento Δr come:

L=F∙Δr = F Δr cos(F,Δr)

                                                                   

 In genere F varia durante lo spostamento: a ogni piccolo spostamento i-esimo Δr_i lungo la traiettoria della massa corrisponderà una forza diversa F(r_i). Il lavoro totale sarà la somma di tutti i singoli lavori  L_i  per gli spostamenti Δr_i :

 dove N è il numero totale di spostamenti  da A a B. Il calcolo del lavoro sarà tanto più preciso quanto più piccoli sono gli intervalli. Per Δr →0 si avrà: 

L(A→B) è il lavoro fatto dalla forza quando la massa passa da A a B lungo il percorso dato. Il lavoro è definito come l’integrale lungo il percorso nello spazio da A a B del prodotto scalare della forza per lo spstamento infinitesimo.

Generalizziamo ora la relazione trovata nel caso unidimensionale.

Scomponiamo la forza F come somma di due vettori componenti F_parall  e F_perp che sono rispettivamente parallelo e perpendicolare allo spostamento:

(solo la componente della forza parallela allo spostamento lavora). La velocità v che compare nelle formule sritte sopra è la velocità scalare lungo la curva.
Dal calcolo vediamo che: Il lavoro compiuto dalla forza F produce una variazione dell'energia cinetica della particella. Con “variazione” dell’energia cinetica si intende l’energia cinetica finale meno quella iniziale.