Problema Momento Angolare

L'esercizio serve per far pratica col calcolo vettoriale e vedere un'applicazione della seconda equazione cardinale dei sistemi.

Problema piattaforma in equilibrio

Nel calcolo si è considerata g = 10 m/s^2.

Problema dinamica e moto relativo

Sopra un piano orizzontale è poggiato un cubo di massa M, che può scorrere senza attrito sul piano orizzontale. Sopra il cubo è poggiato un altro cubetto di massa m a distanza d dalla faccia di sinistra del cubo più grande. All'istante iniziale, quando tutto è fermo, al cubo è applicata una forza F orizzontale. Questa forza è costante; dopo t il cubetto cade. Calcolare il coefficiente di attrito tra i due cubi. (Dati del problema M=50 kg, m=10 kg, d=50 cm, F=100 N, t=2 s)

Problema momento impulso

Una sbarra di lunghezza L=40 cm, di massa trascurabile, che è incernierata ad un estremo ad un perno fisso, può muoversi liberamente in un piano verticale. La sbarra ha attaccata all’altro estremo una massa m di 2.5 kg. La sbarra e la massa sono inizialmente ferme, con l’asta verticale e la massa in basso. La massa riceve un impulso e compie un quarto di giro. Determinare la velocità angolare che assume inizialmente la massa e l'impulso che viene applicato.

Problema dinamica

Una persona si trova su una pedana mobile. Tra la pedana ed il pavimento l’attrito è trascurabile. Tra la persona e la pedana c’è attrito statico. La persona tira la fune e nella fune si sviluppa una tensione T di 20 N. La massa M è di 60 kg, la pedana è di 20 kg. Trovate l’accelerazione di persona e pedana.

La persona non scivola sulla pedana. C'è l'attrito statico che crea la forza A orizzontale. Le due figure con le frecce colorate sono i diagrammi di corpo libero per la persona (M) e per la pedana (m).

Problema dinamica

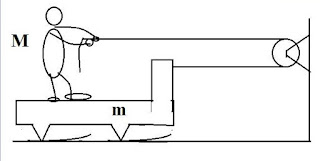
Calcolare l’accelerazione del sistema fatto da una massa m e da una pedana M, come in figura. Il filo è inestensibile e privo di massa, così come la carrucola. La massa mobile è appoggiata alla parete verticale del carrello. Non vi sono attriti.

Problema dinamica

Una persona si trova su una pedana mobile. Tra la pedana ed il pavimento l’attrito è trascurabile. Tra la persona e la pedana c’è attrito statico. La persona tira la fune e nella fune si sviluppa una tensione T di 20 N. La massa M è di 60 kg, la pedana è di 20 kg. Trovate l’accelerazione di persona e pedana.

Pedana M:   M a = T  (verso destra);    M g = N  dove N è l'azione del pavimento

Massa m: ma = mg ─ T (verso il basso) 

La fune  è inestensibile, sommo  equazioni

Ma + ma = T + mg -T = mg

a = mg/(M+m)

Majorana 'zero modes' spotted in superconducting nanowires - physicsworld.com

Majorana 'zero modes' spotted in superconducting nanowires - physicsworld.com

Problema dinamica

Una ragazza di 60 kg sta in piedi su una piattaforma di alluminio di 15 kg per dipingere una casa. Una fune attaccata alla piattaforma e passante su una carrucola fissata al soffitto consente alla ragazza di sollevare se stessa e la piattaforma. (a) Per muoversi la ragazza imprime a se stessa e alla piattaforma un'accelerazione di 0,8 m/s². Con che forza deve tirare la corda? (b) Dopo 1 s la ragazza tira in modo da salire con la piattaforma con la velocità costante di 1 m/s. Che forza deve esercitare sulla corda?
[Ris. (a) 397 N; (b) 367 N.] Vedi anche https://physicstasks.eu/278/boy-on-a-pulley

m _r = 60 kg , m_p = 15 kg , m _tot = 75 kg , a = 0.8 m/s² , g = 9.8 m/s²

A) Sia F la forza applicata F dalla ragazza che tira la fune verso il basso. Sia T la tensione della fune.
Dobbiamo trovare la forza F. Sia la direzione verso l'alto quella positiva. Si ha
F = T (in modulo)

Sulla massa totale: T + F - m_tot g = m_r a 

2 F = m_r (a + g) da cui F = 397 N 

Dove la ragazza applica la forza, si ha in modulo F = T (azione e reazione). La forza F è verso il basso e la reazione è verso l'alto; così la corda agisce sulla ragazza verso l'alto.

B) a=0
F = T
T + F - m_r g = 0
2F = m_r g e quindi: F = 367 N

Problema dinamica

Fate il problema che trovate al link

https://physicstasks.eu/278/boy-on-a-pulley