Un disco di bronzo, un asse di riferimento e un calendario del Nord,
di Amelia Carolina Sparavigna
L’articolo mostra come con un sistema di coordinate polari, che è un sistema di riferimento usato per descrivere il moto dei pianeti, è possibile trasformare la decorazione di un disco solare dell’Età del Bronzo in un calendario.
(in Inglese: Ancient bronze disks, decorations and calendars, at http://arxiv.org/abs/1203.2512)
Alcuni antichi dischi di bronzo, ritrovati in certe sepolture di epoca preistorica in Danimarca, sono coperti da sorprendenti decorazioni, composte di cerchi concentrici, spirali e complesse linee a zig-zag. Secondo l’archeologo Klavs Randsborg alcuni di questi dischi rappresentano il Sole, il potere supremo della cosmologia dell’Età del Bronzo in Danimarca. Vi era una religione basata sul cammino quotidiano del Sole e sulla progressione dell'anno, come scrive Randsborg nel suo articolo “SPIRALS! Calendars in the Bronze Age in Denmark“ del 2010. E' quindi del tutto logico pensare che questi dischi siano anche dei calendari, come l’archeologo propone per diversi oggetti, tra cui il Carro del Sole di Trundholn, un disco di bronzo e una statuetta di un cavallo posti su un carro con ruote a raggi, e il disco di Egtved, prezioso ornamento di una cintura[1]. Io mi limiterò a discutere il disco di Trundholm, proponendo un nuovo calendario di 360 giorni.
Tra gli oggetti funerari della prima età del Bronzo, il Carro del Sole di Trundholm, Figura 1, è sorprendente per il contrasto tra la fine decorazione del disco e le forme stilizzate di carro e cavallo. Questo manufatto è noto anche come Solvognen. La scultura è stata scoperta nel 1902 in una torbiera nella brughiera di Trundholm ed è ora nella collezione del Museo Nazionale di Danimarca a Copenaghen. E 'stato creato con la fusione a cera persa. Il disco ha un diametro di circa 25 cm. In realtà si compone di due dischi di bronzo, tenuti insieme da una flangia esterna, consistente in un anello di bronzo. Uno dei dischi è dorato. Le decorazioni dei dischi sono state probabilmente create con dei punzoni, perché i cerchi concentrici e le spirali che le compongono sono in pratica identici. Le due facce del disco sono ritenute delle rappresentazioni del sole che si muove nel cielo su un carro trainato da un cavallo, da Est a Ovest durante il giorno, mostrando il suo lato luminoso, quello dorato. Come si vede dalla Figura 2, c’è una fascia esterna che rappresenta i raggi solari (la Figura 3 mostra un dettaglio della decorazione). Durante la notte, ritorna da Ovest a Est, mostrando il suo volto oscurato alla Terra. La scultura è datata dal Museo che lo conserva intorno al 1400 a.C..
Sulla faccia dorata del disco vi è un anello compreso tra due grandi cerchi concentrici, decorato con piccoli cerchi concentrici multipli, legati da un motivo ornamentale a "yin e yang" (vedi Figura 4, parte sinistra). L'immagine sulla destra della stessa figura riproduce la faccia notturna del sole. Queste immagini che vi propongo sono degli schemi semplificati rispetto a quelli pubblicati da Randsborg: quelli che nella figura vediamo come dischetti sono delle spirali o dei cerchi concentrici multipli.
Per il lato che rappresenta la faccia oscura del sole, Klaus Randsborg propone un calendario basato sul seguente calcolo. Partendo dal centro del disco, si somma il numero di dischetti in ogni anello, moltiplicato per l'ordine dell'anello, ossia (1x1 + 2x8 + 3x20 + 4x25). Ciò si traduce in un totale di 177, un numero molto vicino al numero di giorni in sei mesi sinodici. Randsborg suppone quindi che le spirali o i cerchi concentrici multipli rappresentino i giorni. L'anello dove il simbolo si trova fornisce il fattore di moltiplicazione.
Io vorrei proporre un'altra interpretazione per la decorazione della Figure 4 della faccia della notte. Secondo me, nella parte interna del disco ci sono i giorni di una "settimana", fatta di 8 giorni. Non considero, per ora, il cerchio centrale più grande degli altri, fatto da molte circonferenze concentriche. Potrebbe essere un simbolo per un cosmo ordinato e armonico, come immaginato dagli antichi greci. Nelle due corone circolari esterne, ci sono le settimane dell'anno, che sono 45. Se moltiplichiamo i giorni della settimana per il numero di settimane, otteniamo 360 giorni. Cioè: (8 giorni) x (45 settimane) = 360 giorni l'anno. Come nell'antico Egitto, l'anno ha 360 giorni: L’Egitto divideva l'anno in 12 mesi di 30 giorni ciascuno, più cinque giorni supplementari. Notiamo che le settimane sono raggruppati nelle corone circolari in due gruppi di 20 e 25: se si considera il solstizio d'inverno come l'inizio dell'anno, i due gruppi di settimane potrebbero avere il significato di stagioni. Nella prima stagione di 20 settimane regna il "sole giovane", poi segue la stagione di un sole "maturo" che poi invecchia, lunga 25 settimane.
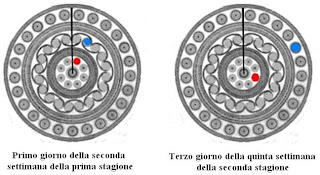
Le settimane di otto giorni sono esistite. Intorno all’ottavo-settimo secolo a.C., gli Etruschi avevano sviluppato il ciclo nundinale, basato su otto giorni la settimana. Questo sistema passò a Roma, che per un certo tempo ebbe un doppio calendario basato su due cicli, uno avente settimane di sette giorni e l'altro avente otto giorni la settimana[2]. In ogni caso, con due markers, uno per il giorno nella parte centrale e un altro per la settimana nella parte esterna, è possibile utilizzare il disco in Figura 5 come un calendario per un sistema nundinale. Naturalmente, abbiamo bisogno di un asse di riferimento, come quello scelto nello schema a destra nella figura. L’esempio in Figura 5 segna il primo giorno della seconda settimana della prima stagione.
Commentiamo ancora il disegno della Figura 5 a destra. Se noi utilizziamo un asse di riferimento, come ad esempio quello scelto in figura, il disco si trasforma in un piano polare, dove l’asse premette di valutate una distanza radiale dal centro del disco e una distanza angolare dall’asse stesso. I concetti di angolo e raggio erano già usati nel primo millennio a.C., ovviamente non nel modo formale che ne facciamo noi. Per rappresentare i cicli della settimana, delle stagioni e dell’anno si può quindi usare un riferimento polare. Il nome di “calendario del Nord” ha perciò un doppio significato, che ci dice che esso apparteneva di una antica popolazione nordica e che esso è basato su un riferimento polare.
Per i cinque giorni extra alla fine dell'anno, si può utilizzare il cerchio al centro del disco. Questo è il centro della rotazione: tutto sta girando attorno ad esso. Questo centro comprende sia la fine che l'inizio dell'anno, in grado di "regolare" il ciclo del tempo, ripristinando l'ordine cosmico. Per quanto riguarda l'altra faccia del disco di Trundholm, quella dorata, posso solo dire che se si considera il numero totale di dischetti (52), quello centrale compreso, e supponendo che ogni dischetto rappresenti una settimana con sette giorni, si ottiene 52 x 7 = 364 giorni. La "settimana" centrale è più grande perché contiene uno o due giorni in più, a secondo gli anni.
E' possibile che il disco Trundholm sia un calendario con due cicli di settinane di 8 e di 7 giorni? La risposta è di là delle mie conoscenze. Personalmente ritengo più probabile il calendario 360 giorni, quello del lato notturno del disco. Naturalmente, il disco potrebbe recare solo delle belle decorazioni. In ogni caso, se cerchiamo di ripeterle, abbiamo bisogno di organizzare per bene la distribuzione di cerchi/spirali, cercando di valutare le distanze relative. Molto probabilmente l'artista possedeva delle conoscenze di geometria che comprendevano la bisezione degli angoli. In Figura 6 ho provato a proporre una possibile organizzazione in settori circolari in fase di progettazione della decorazione.
Per finire, ritengo che sia importante studiare le decorazioni di questi antichi manufatti in bronzo, perché ci possono essere molto utili per comprendere la progressione della conoscenza umana della matematica e della geometria.
1. Trundholm sun chariot http://en.wikipedia.org/wiki/Trundholm_sun_chariot; Klavs Randsborg, SPIRALS! Calendars in the Bronze Age in Denmark
2. Week, http://en.wikipedia.org/wiki/Week, Nundinal cyle, http://en.wikipedia.org/wiki/Roman_calendar#Nundinal_cycle
Fig.1 Il carro del Sole di Trundholm
Fig.2 Il lato dorato del disco solare. Le due facce del disco dono coperte di spirali e cerchi multipli concentrici.
Fig.3 Dettaglio della parte centrale del disco. Notare i cerchi concentrici multipli e le spirali dentro al festone “yin e yang”.
Fig.4 Le decorazioni delle due facce del disco del carro solare
Fig.5. Ecco il calendario del Nord. Nella parte centrale del disco ci sono i giorni di una settimana di 8 giorni. Nei due anelli esterni ci sono le settimane, che sono 45, suddivise in due stagioni di 20 e 25 rispettivamente. Ci sono quindi (8 giorni) x (45 settimane) = 360 giorni dell’anno. A destra vediamo un esempio che mostra marcato il primo giorno della seconda settimana della prima stagione, secondo l’asse di riferimento scelto.
Figura 6 Una possibile suddivisione in settori circolari, per progettare la decorazione del disco.