Velocità e accelerazione in coordinate polari

Velocità e accelerazione in coordinate polari.

  

Abbiamo discusso la velocità e l’accelerazione secondo le coordinate cartesiane ed anche intrinsecamente alla traiettoria. Ora discutiamo come si scrivono utilizzando un riferimento polari.

Immaginiamo di avere una particella che si muove su una certa traiettoria. Noi sappiamo che la sua velocità, come vettore, deve essere tangente la traiettoria. Passiamo ora a scomporre questa velocità secondo due direzioni, che sono quella radiale, ossia del raggio vettore che va dal polo O alla posizione P della particella, e quella trasversa, che corrisponde all’incremento dell’azimut, l’angolo che c’è la direzione radiale e l’asse di riferimento OX. Notiamo che queste direzioni NON sono legate alle direzioni intrinseche alla traiettoria (tangente e centripeta). La direzione radiale e quella trasversa sono tra di loro perpendicolari.

Dato che le due direzioni, radiale e trasversa, sono perpendicolari l’una all’altra, abbiamo che la velocità ha due componenti: quella radiale e quella trasversa. Ossia la velocità della particella è un vettore somma di due vettori componenti come nella figura seguente:

 Dimostriamo che:

Indichiamo in una figura le direzioni del vettori unitari e scriviamo come si può esprimere il raggio vettore da O a P secondo. Esso è il prodotto del modulo r, distanza di P da O, e del suo vettore unitario (versore).

 Deriviamo il raggio vettore secondo il tempo.

Che è ciò che volevamo dimostrare. Abbiamo utilizzato la derivata del versore radiale. Ricordiamoci che la derivata di un vettore che ha  modulo costante è sempre un vettore perpendicolare al vettore da derivare. La derivata del versore radiale è quindi pari al versore trasverso, moltiplicato per la derivata dellìangolo rispetto al tempo. Quanto vale la derivata del versore trasversale? Vediamolo nella seguente figura.

La derivata del versore trasverso deve essere un vettore a esso perpendicolare. E' quindi il versore radiale, cambiato di segno, moltiplicato per la derivata dell'angolo rispetto al tempo.
Utilizzando questo risultato, svolgiamo i calcoli:

Quindi abbiamo che: 

Oscillatore smorzato

Un oscillatore armonico è un sistema che, se spostato dalla sua posizione di equilibrio, sperimenta una forza di richiamo F proporzionale allo spostamento x secondo la legge di Hooke: F=−kx dove k è una costante positiva. Se F è l'unica forza che agisce sul sistema, il sistema è detto oscillatore armonico semplice, ed è sottoposto al moto armonico semplice: oscillazioni sinusoidali attorno al punto di equilibrio, con un’ampiezza costante e una frequenza costante (che non dipende dall'ampiezza). Se una forza di attrito (smorzamento) proporzionale alla velocità è anche presente, l'oscillatore armonico è descritto come un oscillatore smorzato. In tale situazione, la frequenza delle oscillazioni è più piccola rispetto al caso non smorzato, e l'ampiezza delle oscillazioni diminuisce con il tempo. Se una forza esterna dipendente dal tempo è presente, l'oscillatore armonico è descritto come un oscillatore forzato. L'oscillatore armonico semplice non ha alcuna forza motrice e nessun attrito (smorzamento), quindi la forza netta è solo F=−kx. Usando la seconda legge di Newton: F=ma, otteniamo:

Definiamo ω_o² =k/m, l’equazione si scrive allora:

La soluzione generale è: x=Acos(ω_ot+ф), dove l’ampiezza è A e la fase iniziale ф, che soddisfano le condizione iniziali. Un oscillatore armonico forzato è dato dall'equazione: 

.dove  A₀ è l’ampiezza della forzante ed ω_f  è la pulsazione della forzante.

Lo smorzamento può essere visto come una forza sincrona alla velocità ma opposta in verso. Per smorzamento si può quindi assumere la forza F legata a v da F=−cv dove c è il coefficiente di attrito viscoso, dato in newton-secondo/metro.

 

Nell’oscillatore smorzato la massa è attaccata ad una molla e ad uno smorzatore (damper). Nell’equazione seguente, il coefficiente di smorzamento è rappresentato da b.

Un oscillatore armonico smorzato soddisfa l’equazione:

 

 dove b è determinato sperimentalmente dalla relazione  F = − bv. Un esempio è un oscillatore posto sott’acqua, se si suppone che la forza esercitata dall’acqua sia lineare in v.  La pulsazione dell’oscillatore smorzato è: 

 dove Ξ=b/2m. La pulsazione data dalla radice quadrata si dice pulsazione ridotta.

Per trovare questo risultato applichiamo il metodo di soluzione dell’equazione tramite i numeri complessi. Proponiamo che la soluzione sia:

Sostituisco nell’eq(*):

Per essere soddisfatta l’equazione, il numero complesso in parentesi quadra deve essere nullo. Devono essere nulle quindi la parte reale e la parte immaginaria.

.da cui si ricava che il coefficiente di smorzamento dell ampiezza e: μ=b/(2m).

Inoltre

da cui la pulsazione ridotta data sopra.

Notiamo che quest'ultima equazione può dar luogo a pulsazioni reali oppure a pulsazioni immaginarie. Nel caso che   ω_o  è maggiore di b/2m, allora    ω è reale e la soluzione è un'oscillazione smorzata. Se invece   ω_o  è minore o uguale a b/2m, allora    ω è complessa e pari a   ω =i q; la soluzione è un esponente decrescente e si dice che il moto e "sovrasmorzato". 

Forza elastica

Un materiale si dice elastico se si deforma sotto stress (ad esempio, sotto l’azione di forze esterne) ma poi ritorna alla sua forma originale quando lo stress è rimosso. La deformazione è detta in Inglese “strain”. Il regime elastico è caratterizzato da una relazione lineare tra forza applicata e deformazione, detta elasticità lineare. Questa legge è stata ricavata da Robert Hooke nel 1676. Il modello classico di elasticità lineare è la molla perfetta. Nella maggior parte dei casi, i materiali sono elastici solo per piccole deformazioni. Le molle sono solitamente realizzate in acciaio temprato.

La costante della molla (rigidità) è la forza applicata divisa per la quantità di deformazione. Per una molla di trazione o compressione, la costante ha l'unità di N/m, o simili. Molle che non siano allungate o compresse oltre il loro limite elastico seguono la legge di Hooke, che afferma che la forza con cui la molla reagice è direttamente proporzionale alla differenza della sua lunghezza da quella che ha a riposo: F=−kx, x=L−Lo. La costante della molla è k.

La figura seguente mostra la molla a riposo.

Se scegliamo l’asse come in figura, con l’origine nella posizione del’estremo della molla a riposo, abbiamo la legge di Hooke scritta proprio come F=−kx, perché x si identifica con la deformazione della molla. Il segno meno indica che la molla agisce con una forza come indicato nella figura seguente. Se la molla è allungata, la forza richiama verso l’origine. Se la molla viene compressa, la forza della molla spinge verso l’origine.

Se alla molla è attaccata una massa e se tra la massa e  il piano orizzontale non c’è attrito, allora l’equazione della dinamica cui obbedisce la massa è: F=−kx=m a, per piccole deformazioni della molla. Infatti, se spostiamo la massa dalla posizione di equilibrio di una quantità x sappiamo che su di essa agisce una forza di richiamo F=−kx. L'equazione del moto è quindi:

                                                         

Un’equazione simile l’abbiamo incontrata studiando il pendolo. Esso è una particella di massa m appesa tramite una fune inestensibile e di massa trascurabile. Se spostiamo il punto dalla verticale, esso inizia ad oscillare intorno alla verticale. Sulla massa agiscono la tensione della fune ed il peso.

  

Per le piccole oscillazioni, indicando con θ l’angolo formato dal filo con la verticale, l’equazione della dinamica del pendolo è:  

La pulsazione del pendolo è Ω²=g/L, dove L è la lunghezza del filo e g l’accelerazione di gravità.  La soluzione dell'equazione è del tipo: θ=θo cos(Ωt+ф), dove θo è detta ampiezza e ф  è la fase iniziale. Questi due parametri sono determinati dalla condizione iniziale del moto. Il periodo di oscillazione del pendolo dipende solo dalla lunghezza del filo e dall'accelerazione di gravità.

Torniamo alla massa vincolata dalla molla alla parete. L'equazione del moto è:

Questa equazione è la stessa di quella del pendolo se al posto di x pensiamo di avere l'angolo θ e al posto del rapporto k/m il rapporto L/g. La soluzione allora sarà:

dove Ω²=k/m. La dinamica del sistema vincola la pulsazione ad  uno specifico valore. Esso non dipende dalle condizioni iniziali del moto e quindo non dipende dall’ampiezza xo, e dalla fase iniziale, ф.

Oscillatore forzato

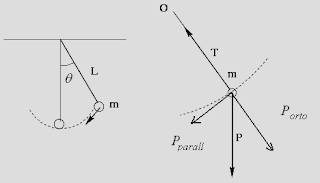
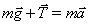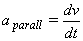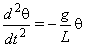L'oscillatore armonico semplice è determinato dall'equazione del moto: m a(t) + k x(t) = 0, che descrive il moto prodotto da una forza di richiamo elastica proporzionale allo spostamento della massa m dall'origine delle coordinate. a(t) indica l'accelerazione istantanea ed è pari alla derivata seconda di x rispetto al tempo.

La legge di questo moto è:

x(t)=A cos (ω_ot + φ)

dove ω_o = √(k/m) è la pulsazione propria (o naturale) dell'oscillazione libera, mentre A e φ sono due costanti che dipendono dalle condizioni iniziali del moto. Siamo ora  interessati all'oscillatore forzato, che è un oscillatore armonico al quale si applica, oltre alla forza elastica, anche una forza esterna, armonica anch'essa, di frequenza arbitraria. L'equazione del moto diviene

m a(t) + k x(t) = F(t)

dove F(t)=Fo cos(ωt), è appunto la forza esterna. Assumiamo che il moto risultante sia ancora un moto armonico, e sostituiamo nell'equazione del moto la soluzione di prova:

x(t)=A cos (ωt)

Otteniamo l'equazione (-m ω²+k) A cos (ωt) = Fo cos(ωt), da cui otteniamo l'ampiezza del moto risultante in funzione dell'ampiezza Fo della forza applicata, e della pulsazione: 

La regione attorno ad ω₀  è la regione in cui si ha una risonanza. La risonanza corrisponde ad un massimo dell’ampiezza. Anzi, nel caso che stiamo studiando c'è una divergenza. 

Studiando l'ampiezza dell'oscillazione come funzione della pulsazione della forza esterna appaiono immediate alcune considerazioni.

a) Data l'intensità della forza esterna, l'ampiezza delle oscillazioni è tanto maggiore quanto più la pulsazione della forza esterna ω è vicina alla pulsazione propria ω₀ dell'oscillatore.

b) Pulsazioni molto maggiori o molto minori di ω₀ tendono a ridurre l'ampiezza delle oscillazioni.

c) Per pulsazioni prossime ad ω₀ avviene un fenomeno legato all’energia. L'energia della sorgente esterna si trasferisce in modo sempre più efficiente all'oscillatore, accumulandosi di periodo in periodo provocando oscillazioni sempre maggiori.

d) A ω = ω₀ le oscillazioni diventano di ampiezza infinita. Nella realtà ciò non accade perché ci sono fenomeni di smorzamento.

Finora si è considerato l'oscillatore soggetto solamente alla forza di richiamo elastica e alla forza esterna periodica F(t)=F₀cos(ωt). Nelle situazioni reali i sistemi oscillanti sono soggetti a fenomeni dissipativi, che smorzano cioè l'ampiezza delle oscillazioni dissipando energia. Ci possono essere diversi effetti dissipativi, quali l'attrito radente (se la massa scivola su di una superficie di appoggio scabra), all'attrito tra parti interne del sistema oscillante, all'attrito che il sistema incontra per la presenza di un mezzo viscoso. Quest’ultimo attrito  è  descrivibile per basse velocità da un'espressione del tipo:

F_attr= − γ v(t)=  − γ dx(t)/dt 

L'equazione del moto diviene

 m a(t)= F(t) − kx(t)  − γ v(t)  (*)

dove, a secondo membro, abbiamo messo la forza totale agente sull'oscillatore.
L'equazione è quindi:



Per determinare una soluzione della nuova equazione, assumiamo stavolta una soluzione di prova 

 x(t) = A cos (ωt+ф)

con l'idea di determinare le costanti A e ф  in modo che essa fornisca una soluzione dell'equazione del moto (*). Ricordiamo che ω_o = √(k/m). Dopo una serie di derivazione e sostituzioni, si arriva al risultato che:

Ancora una volta forza e posizione x non sono in fase tra loro.

Per pulsazioni della forzante molto diverse dalla pulsazione propria dell'oscillatore l'ampiezza delle oscillazioni resta piccola. Man mano che ci si avvicina alla risonanza la risposta dell'oscillatore diventa sempre più grande. Essa non è infinita  ma raggiunge un massimo, determinato dal coefficiente di attrito del sistema. Il coefficiente d'attrito provoca  un piccolo cambiamento della frequenza di risonanza del sistema. La “risonanza dell’ampiezza” si ha per la pulsazione: 

.

Quindi la pulsazione di risonanza dell’ampiezza diminuisce all'aumentare dell'attrito. Il massimo dell'ampiezza si ha per una pulsazione forzante che è minore della pulsazione propria del sistema. Il picco di risonanza è sempre a sinistra della linea verticale corrispondente  alla pulsazione propria del sistema.

In genere la differenza tra la frequenza della risonanza dell'ampiezza e quella proria è piccola perché γ ha valori numerici molto piccoli rispetto a m e k.

L’andamento dello sfasamento è come mostrato nella seguente figura.

La “risonanza della fase” è sempre a -π/2. Quando siamo a questa risonanza, la forza che agisce sul sistema e la velocità risultano in fase. Infatti: x=A cos (ωt - pigreco/2). La velocità è dx/dt=Aωcos(ωt). Siccome la potenza è il prodotto della velocità per la forza, la potenza massima assorbità ci sarà quando queste due grandezze sono in fase.

Domanda di teoria - pendolo

Discutete il pendolo

Si prenda un punto materiale di massa m appeso tramite una fune inestensibile e di massa trascurabile: esso costituisce il cosiddetto pendolo semplice. Se spostiamo il punto dalla verticale, esso inizia ad oscillare intorno a questa posizione che è la posizione di equilibrio. Studiamo il moto della massa.

Le forze che agiscono sulla massa sono il peso e la tensione della fune.

L'accelerazione è in parte parallela ed in parte ortogonale alla traiettoria, poiché la risultante R vettoriale delle forze ha componenti parallela ed ortogonale:

Il segno negativo  (-mg sin θ= m a_parall) deriva dal fatto che la forza si oppone alla crescita dell'angolo θ: è quindi una forza di richiamo. Sappiamo, dallo studio della cinematica, che l'accelerazione ortogonale alla traiettoria è l'accelerazione centripeta: 

                                                          

L'accelerazione parallela è quella tangenziale: 

che è la derivata della velocità lungo la linea (velocità scalare, data dall'incremento dell'arco rispetto al tempo). Ricordiamo che la velocità lineare è legata alla velocità angolare dalla relazione:

In questa equazione L è la lunghezza del filo che è anche il raggio della circonferenza cui l'arco della traiettoria del pendolo appartiene. Ricordiamo che dθ/dt è la velocità angolare. Quindi l’accelerazione parallela è:

L’equazione per la componente parallela alla traiettoria diventa:

dove abbiamo semplificato  la massa e diviso per L.

Se θ è piccolo, è possibile confondere il seno con l'angolo stesso: sinθ=θ, e quindi: 

Poniamo 

La soluzione dell'equazione è del tipo: θ=θ_o cos(ωt+ф), dove θ_o è detta ampiezza e ф è la fase iniziale. Verifichiamo che questa è soluzione dell'equazione, calcolando la derivata seconda dell'angolo:

E quindi si verifica l’equazione. I parametri θo e φ dipendono dalla condizione iniziale del moto. Supposiamo che al tempo t=0, il pendolo formi un angolo  Θ  rispetto alla verticale, allora:

L’angolo iniziale è dato dall’ ampiezza moltiplicata per il coseno della fase iniziale.

Immaginiamo ora di lasciar andare la massa da ferma: la  fase iniziale è nulla e Θ=θo.

Allora possiamo descrivere il moto con la funzione: 

  

Il periodo delle oscillazioni è il periodo della funzione coseno: 

Il periodo di oscillazione del pendolo dipende dalla lunghezza del filo e dall'accelerazione di gravità. Non dipende dalla massa e dal valore di θ_o.

L’equazione che abbiamo trovato per le piccole oscillazioni del pendolo è una equazione armonica: è la stessa equazione che descrive il moto di una massa vincolata ad una molla. Spostando la massa dalla posizione di equilibrio di una quantità x sappiamo che su di essa agisce una forza di richiamo F=-kx.,  dove k è la costante elastica della molla. L'equazione del moto è quindi:

Ma questa equazione è la stessa che abbiamo già incontrato per il pendolo se al posto di x pensiamo di avere l'angolo θ e al posto del rapporto k/m il rapporto L/g. La soluzione allora sarà: