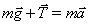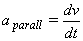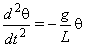Discutete il pendolo
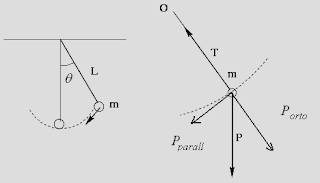
Si prenda un punto materiale di massa m appeso tramite una fune inestensibile e di massa trascurabile: esso costituisce il cosiddetto pendolo semplice. Se spostiamo il punto dalla verticale, esso inizia ad oscillare intorno a questa posizione che è la posizione di equilibrio. Studiamo il moto della massa.
Le forze che agiscono sulla massa sono il peso e la tensione della fune.
L'accelerazione è in parte parallela ed in parte ortogonale alla traiettoria, poiché la risultante R vettoriale delle forze ha componenti parallela ed ortogonale:
Il segno negativo (-mg sin θ= m aparall) deriva dal fatto che la forza si oppone alla crescita dell'angolo θ: è quindi una forza di richiamo. Sappiamo, dallo studio della cinematica, che l'accelerazione ortogonale alla traiettoria è l'accelerazione centripeta:
L'accelerazione parallela è quella tangenziale:
che è la derivata della velocità lungo la linea (velocità scalare, data dall'incremento dell'arco rispetto al tempo). Ricordiamo che la velocità lineare è legata alla velocità angolare dalla relazione:
In questa equazione L è la lunghezza del filo che è anche il raggio della circonferenza cui l'arco della traiettoria del pendolo appartiene. Ricordiamo che dθ/dt è la velocità angolare. Quindi l’accelerazione parallela è:
L’equazione per la componente parallela alla traiettoria diventa:
dove abbiamo semplificato la massa e diviso per L.
Se θ è piccolo, è possibile confondere il seno con l'angolo stesso: sinθ=θ, e quindi:
Poniamo
La soluzione dell'equazione è del tipo: θ=θo cos(ωt+ф), dove θo è detta ampiezza e ф è la fase iniziale. Verifichiamo che questa è soluzione dell'equazione, calcolando la derivata seconda dell'angolo:
E quindi si verifica l’equazione. I parametri θo e φ dipendono dalla condizione iniziale del moto. Supposiamo che al tempo t=0, il pendolo formi un angolo Θ rispetto alla verticale, allora:
L’angolo iniziale è dato dall’ ampiezza moltiplicata per il coseno della fase iniziale.
Immaginiamo ora di lasciar andare la massa da ferma: la fase iniziale è nulla e Θ=θo.
Allora possiamo descrivere il moto con la funzione:
Il periodo delle oscillazioni è il periodo della funzione coseno:
Il periodo di oscillazione del pendolo dipende dalla lunghezza del filo e dall'accelerazione di gravità. Non dipende dalla massa e dal valore di θo.
L’equazione che abbiamo trovato per le piccole oscillazioni del pendolo è una equazione armonica: è la stessa equazione che descrive il moto di una massa vincolata ad una molla. Spostando la massa dalla posizione di equilibrio di una quantità x sappiamo che su di essa agisce una forza di richiamo F=-kx., dove k è la costante elastica della molla. L'equazione del moto è quindi:
Ma questa equazione è la stessa che abbiamo già incontrato per il pendolo se al posto di x pensiamo di avere l'angolo θ e al posto del rapporto k/m il rapporto L/g. La soluzione allora sarà: