Abbiamo visto discutendo la derivata della velocità che se u è un vettore unitario (detto anche versore):
è un vettore perpendicolare (normale) a u. Nella figura seguente il vettore normale è chiamato n.
Il modulo di questa derivata è dato da:
Consideriamo il piano dell’angolo ed il vettore velocità angolare ad esso perpendicolare. Il vettore unitario ruota attorno ad esso, come in figura.
Possiamo quindi dire che:
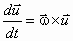
Vettori unitari sono quei vettori che danno le direzioni dei tre assi cartesiani. Supponiamo un riferimento ruotante nello spazio con vettori unitari i’,j’,k’.
Le derivate di questi vettori sono allora:
Prendiamo ora un riferimento fisso ed un riferimento, solo ruotante, con velocita’ angolare w costante. I riferimenti siano cartesiani. Per semplificare il calcolo pensiamo a scegliere le origini dei due riferimenti, O e O’, come coincidenti. Fissato un punto P, il vettore posizione puo’ essere dato rispetto ad O oppure rispetto a O’.
Adesso calcoliamo la derivata rispetto al tempo del vettore posizione, ricordando che x,y,z sono funzioni del tempo, i,j,k, sono fissi, x’,y’,z’ sono variabili nel tempo ed infine i’,j’,k’ che ruotando sono anche loro funzioni del tempo.

Si possono calcolare le accelerazioni nella stessa maniera e si ottiene:

L’accelerazione osservata nel riferimento fisso è uguale a quella osservata nel sistema rotante più il termine di Coriolis più il termine centripeto.
Facciamo un esempio. Immaginiamo di avere un punto fisso P nel riferimento fisso (quello che a lezione abbiamo detto essere dell'osservatore Joe). Con che velocita’ Moe (l'osservatore nel sistema ruotante, ad esempio su una piattaforma rotante) vede muoversi P? Uso la relazione della velocità:
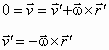
Se la piattaforma ruota in senso orario, Moe vede il punto ruotare in verso antiorario.
Passiamo all’accelerazione:
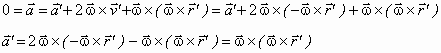
Moe vede il punto P che ruotando ha una accelerazione centripeta.
Dimostrazioni delle formule:









