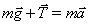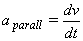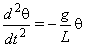Forza elastica

Un materiale si dice elastico se si deforma sotto stress (ad esempio, sotto l’azione di forze esterne) ma poi ritorna alla sua forma originale quando lo stress è rimosso. La deformazione è detta in Inglese “strain”. Il regime elastico è caratterizzato da una relazione lineare tra forza applicata e deformazione, detta elasticità lineare. Questa legge è stata ricavata da Robert Hooke nel 1676. Il modello classico di elasticità lineare è la molla perfetta. Nella maggior parte dei casi, i materiali sono elastici solo per piccole deformazioni. Le molle sono solitamente realizzate in acciaio temprato.

La costante della molla (rigidità) è la forza applicata divisa per la quantità di deformazione. Per una molla di trazione o compressione, la costante ha l'unità di N/m, o simili. Molle che non siano allungate o compresse oltre il loro limite elastico seguono la legge di Hooke, che afferma che la forza con cui la molla reagice è direttamente proporzionale alla differenza della sua lunghezza da quella che ha a riposo: F=−kx, x=L−Lo. La costante della molla è k.

La figura seguente mostra la molla a riposo.

Se scegliamo l’asse come in figura, con l’origine nella posizione del’estremo della molla a riposo, abbiamo la legge di Hooke scritta proprio come F=−kx, perché x si identifica con la deformazione della molla. Il segno meno indica che la molla agisce con una forza come indicato nella figura seguente. Se la molla è allungata, la forza richiama verso l’origine. Se la molla viene compressa, la forza della molla spinge verso l’origine.

Se alla molla è attaccata una massa e se tra la massa e  il piano orizzontale non c’è attrito, allora l’equazione della dinamica cui obbedisce la massa è: F=−kx=m a, per piccole deformazioni della molla. Infatti, se spostiamo la massa dalla posizione di equilibrio di una quantità x sappiamo che su di essa agisce una forza di richiamo F=−kx. L'equazione del moto è quindi:

                                                         

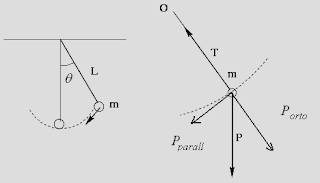
Un’equazione simile l’abbiamo incontrata studiando il pendolo. Esso è una particella di massa m appesa tramite una fune inestensibile e di massa trascurabile. Se spostiamo il punto dalla verticale, esso inizia ad oscillare intorno alla verticale. Sulla massa agiscono la tensione della fune ed il peso.

  

Per le piccole oscillazioni, indicando con θ l’angolo formato dal filo con la verticale, l’equazione della dinamica del pendolo è:  

La pulsazione del pendolo è Ω²=g/L, dove L è la lunghezza del filo e g l’accelerazione di gravità.  La soluzione dell'equazione è del tipo: θ=θo cos(Ωt+ф), dove θo è detta ampiezza e ф  è la fase iniziale. Questi due parametri sono determinati dalla condizione iniziale del moto. Il periodo di oscillazione del pendolo dipende solo dalla lunghezza del filo e dall'accelerazione di gravità.

Torniamo alla massa vincolata dalla molla alla parete. L'equazione del moto è:

Questa equazione è la stessa di quella del pendolo se al posto di x pensiamo di avere l'angolo θ e al posto del rapporto k/m il rapporto L/g. La soluzione allora sarà:

dove Ω²=k/m. La dinamica del sistema vincola la pulsazione ad  uno specifico valore. Esso non dipende dalle condizioni iniziali del moto e quindo non dipende dall’ampiezza xo, e dalla fase iniziale, ф.

Oscillatore forzato

L'oscillatore armonico semplice è determinato dall'equazione del moto: m a(t) + k x(t) = 0, che descrive il moto prodotto da una forza di richiamo elastica proporzionale allo spostamento della massa m dall'origine delle coordinate. a(t) indica l'accelerazione istantanea ed è pari alla derivata seconda di x rispetto al tempo.

La legge di questo moto è:

x(t)=A cos (ω_ot + φ)

dove ω_o = √(k/m) è la pulsazione propria (o naturale) dell'oscillazione libera, mentre A e φ sono due costanti che dipendono dalle condizioni iniziali del moto. Siamo ora  interessati all'oscillatore forzato, che è un oscillatore armonico al quale si applica, oltre alla forza elastica, anche una forza esterna, armonica anch'essa, di frequenza arbitraria. L'equazione del moto diviene

m a(t) + k x(t) = F(t)

dove F(t)=Fo cos(ωt), è appunto la forza esterna. Assumiamo che il moto risultante sia ancora un moto armonico, e sostituiamo nell'equazione del moto la soluzione di prova:

x(t)=A cos (ωt)

Otteniamo l'equazione (-m ω²+k) A cos (ωt) = Fo cos(ωt), da cui otteniamo l'ampiezza del moto risultante in funzione dell'ampiezza Fo della forza applicata, e della pulsazione: 

La regione attorno ad ω₀  è la regione in cui si ha una risonanza. La risonanza corrisponde ad un massimo dell’ampiezza. Anzi, nel caso che stiamo studiando c'è una divergenza. 

Studiando l'ampiezza dell'oscillazione come funzione della pulsazione della forza esterna appaiono immediate alcune considerazioni.

a) Data l'intensità della forza esterna, l'ampiezza delle oscillazioni è tanto maggiore quanto più la pulsazione della forza esterna ω è vicina alla pulsazione propria ω₀ dell'oscillatore.

b) Pulsazioni molto maggiori o molto minori di ω₀ tendono a ridurre l'ampiezza delle oscillazioni.

c) Per pulsazioni prossime ad ω₀ avviene un fenomeno legato all’energia. L'energia della sorgente esterna si trasferisce in modo sempre più efficiente all'oscillatore, accumulandosi di periodo in periodo provocando oscillazioni sempre maggiori.

d) A ω = ω₀ le oscillazioni diventano di ampiezza infinita. Nella realtà ciò non accade perché ci sono fenomeni di smorzamento.

Finora si è considerato l'oscillatore soggetto solamente alla forza di richiamo elastica e alla forza esterna periodica F(t)=F₀cos(ωt). Nelle situazioni reali i sistemi oscillanti sono soggetti a fenomeni dissipativi, che smorzano cioè l'ampiezza delle oscillazioni dissipando energia. Ci possono essere diversi effetti dissipativi, quali l'attrito radente (se la massa scivola su di una superficie di appoggio scabra), all'attrito tra parti interne del sistema oscillante, all'attrito che il sistema incontra per la presenza di un mezzo viscoso. Quest’ultimo attrito  è  descrivibile per basse velocità da un'espressione del tipo:

F_attr= − γ v(t)=  − γ dx(t)/dt 

L'equazione del moto diviene

 m a(t)= F(t) − kx(t)  − γ v(t)  (*)

dove, a secondo membro, abbiamo messo la forza totale agente sull'oscillatore.
L'equazione è quindi:



Per determinare una soluzione della nuova equazione, assumiamo stavolta una soluzione di prova 

 x(t) = A cos (ωt+ф)

con l'idea di determinare le costanti A e ф  in modo che essa fornisca una soluzione dell'equazione del moto (*). Ricordiamo che ω_o = √(k/m). Dopo una serie di derivazione e sostituzioni, si arriva al risultato che:

Ancora una volta forza e posizione x non sono in fase tra loro.

Per pulsazioni della forzante molto diverse dalla pulsazione propria dell'oscillatore l'ampiezza delle oscillazioni resta piccola. Man mano che ci si avvicina alla risonanza la risposta dell'oscillatore diventa sempre più grande. Essa non è infinita  ma raggiunge un massimo, determinato dal coefficiente di attrito del sistema. Il coefficiente d'attrito provoca  un piccolo cambiamento della frequenza di risonanza del sistema. La “risonanza dell’ampiezza” si ha per la pulsazione: 

.

Quindi la pulsazione di risonanza dell’ampiezza diminuisce all'aumentare dell'attrito. Il massimo dell'ampiezza si ha per una pulsazione forzante che è minore della pulsazione propria del sistema. Il picco di risonanza è sempre a sinistra della linea verticale corrispondente  alla pulsazione propria del sistema.

In genere la differenza tra la frequenza della risonanza dell'ampiezza e quella proria è piccola perché γ ha valori numerici molto piccoli rispetto a m e k.

L’andamento dello sfasamento è come mostrato nella seguente figura.

La “risonanza della fase” è sempre a -π/2. Quando siamo a questa risonanza, la forza che agisce sul sistema e la velocità risultano in fase. Infatti: x=A cos (ωt - pigreco/2). La velocità è dx/dt=Aωcos(ωt). Siccome la potenza è il prodotto della velocità per la forza, la potenza massima assorbità ci sarà quando queste due grandezze sono in fase.

Domanda di teoria - pendolo

Discutete il pendolo

Si prenda un punto materiale di massa m appeso tramite una fune inestensibile e di massa trascurabile: esso costituisce il cosiddetto pendolo semplice. Se spostiamo il punto dalla verticale, esso inizia ad oscillare intorno a questa posizione che è la posizione di equilibrio. Studiamo il moto della massa.

Le forze che agiscono sulla massa sono il peso e la tensione della fune.

L'accelerazione è in parte parallela ed in parte ortogonale alla traiettoria, poiché la risultante R vettoriale delle forze ha componenti parallela ed ortogonale:

Il segno negativo  (-mg sin θ= m a_parall) deriva dal fatto che la forza si oppone alla crescita dell'angolo θ: è quindi una forza di richiamo. Sappiamo, dallo studio della cinematica, che l'accelerazione ortogonale alla traiettoria è l'accelerazione centripeta: 

                                                          

L'accelerazione parallela è quella tangenziale: 

che è la derivata della velocità lungo la linea (velocità scalare, data dall'incremento dell'arco rispetto al tempo). Ricordiamo che la velocità lineare è legata alla velocità angolare dalla relazione:

In questa equazione L è la lunghezza del filo che è anche il raggio della circonferenza cui l'arco della traiettoria del pendolo appartiene. Ricordiamo che dθ/dt è la velocità angolare. Quindi l’accelerazione parallela è:

L’equazione per la componente parallela alla traiettoria diventa:

dove abbiamo semplificato  la massa e diviso per L.

Se θ è piccolo, è possibile confondere il seno con l'angolo stesso: sinθ=θ, e quindi: 

Poniamo 

La soluzione dell'equazione è del tipo: θ=θ_o cos(ωt+ф), dove θ_o è detta ampiezza e ф è la fase iniziale. Verifichiamo che questa è soluzione dell'equazione, calcolando la derivata seconda dell'angolo:

E quindi si verifica l’equazione. I parametri θo e φ dipendono dalla condizione iniziale del moto. Supposiamo che al tempo t=0, il pendolo formi un angolo  Θ  rispetto alla verticale, allora:

L’angolo iniziale è dato dall’ ampiezza moltiplicata per il coseno della fase iniziale.

Immaginiamo ora di lasciar andare la massa da ferma: la  fase iniziale è nulla e Θ=θo.

Allora possiamo descrivere il moto con la funzione: 

  

Il periodo delle oscillazioni è il periodo della funzione coseno: 

Il periodo di oscillazione del pendolo dipende dalla lunghezza del filo e dall'accelerazione di gravità. Non dipende dalla massa e dal valore di θ_o.

L’equazione che abbiamo trovato per le piccole oscillazioni del pendolo è una equazione armonica: è la stessa equazione che descrive il moto di una massa vincolata ad una molla. Spostando la massa dalla posizione di equilibrio di una quantità x sappiamo che su di essa agisce una forza di richiamo F=-kx.,  dove k è la costante elastica della molla. L'equazione del moto è quindi:

Ma questa equazione è la stessa che abbiamo già incontrato per il pendolo se al posto di x pensiamo di avere l'angolo θ e al posto del rapporto k/m il rapporto L/g. La soluzione allora sarà: 

Moti Relativi - sistemi fisso e rotante

Relazioni di velocità e accelerazione tra riferimento fisso e riferimento ruotante con velocità angolare costante.

Abbiamo visto discutendo la derivata della velocità che se u è un vettore unitario (detto anche versore):

è un vettore perpendicolare (normale) a u. Nella figura seguente il vettore normale è chiamato n.
Il modulo di questa derivata è dato da:

che è la velocità angolare.

Consideriamo il piano dell’angolo ed il vettore velocità angolare ad esso perpendicolare. Il vettore unitario ruota attorno ad esso, come in figura.

Possiamo quindi dire che:



Vettori unitari sono quei vettori che danno le direzioni dei tre assi cartesiani. Supponiamo un riferimento ruotante nello spazio con vettori unitari i’,j’,k’.

Le derivate di questi vettori sono allora:

Prendiamo ora un riferimento fisso ed un riferimento, solo ruotante, con velocita’ angolare w costante. I riferimenti siano cartesiani. Per semplificare il calcolo pensiamo a scegliere le origini dei due riferimenti, O e O’, come coincidenti. Fissato un punto P, il vettore posizione puo’ essere dato rispetto ad O oppure rispetto a O’.

Adesso calcoliamo la derivata rispetto al tempo del vettore posizione, ricordando che x,y,z sono funzioni del tempo, i,j,k, sono fissi, x’,y’,z’ sono variabili nel tempo ed infine i’,j’,k’ che ruotando sono anche loro funzioni del tempo.



Si possono calcolare  le accelerazioni nella stessa maniera e si ottiene:



L’accelerazione osservata nel riferimento fisso è uguale a quella osservata nel sistema rotante più il termine di Coriolis più il termine centripeto.

Facciamo un esempio. Immaginiamo di avere un punto fisso P nel riferimento fisso (quello che a lezione abbiamo detto essere dell'osservatore Joe). Con che velocita’ Moe (l'osservatore nel sistema ruotante, ad esempio su una piattaforma rotante) vede muoversi P? Uso la relazione della velocità:



Se la piattaforma ruota in senso orario, Moe vede il punto ruotare in verso antiorario.
Passiamo all’accelerazione:



Moe vede il punto P che ruotando ha una accelerazione centripeta.

Dimostrazioni delle formule:

Escavatore

Da Wikipedia "Un escavatore è una macchina utilizzata per tutte le operazioni che richiedono un movimento di terra, ovvero la rimozione di porzioni di terreno non particolarmente coerente, tale da consentirne una relativamente facile frantumazione. L'operatore che aziona la macchina viene definito escavatorista. Il primo escavatore (o pala meccanica) venne costruito da William Otis nel 1837."
Non è proprio così. Guardate il seguente disegno di Giovanni Fontana

Johannes de Fontana: Bellicorum instrumentorum liber cum figuris
BSB Cod.icon. 242 Venedig 1420 - 1430
http://en.wikipedia.org/wiki/Giovanni_Fontana_(engineer)

Macchina a reazione

Johannes de Fontana: Bellicorum instrumentorum liber cum figuris
BSB Cod.icon. 242 Venedig 1420 - 1430

http://en.wikipedia.org/wiki/Giovanni_Fontana_(engineer)

Coriolis

Artillery and Coriolis   ... "The military apparatus of Napoleon's era observed that the new long-range cannon landed their missiles always to the right when accurately trained on the target before firing. The apparent deflection of the missile from the straight path between gun and target was explained by Gustave Gaspard Coriolis  as due to the movement of the Earth, and therefore the target, whilst the missile was in flight. ... However, the story is improbable"
http://www-das.uwyo.edu/~geerts/cwx/notes/chap11/artillery.html

Starting motion

Very good discussion about starting motion

http://electron6.phys.utk.edu/101/CH2/wheels.htm

What makes the car start moving forward? Let us, for the moment, forget about the details of the engine and the transmission.  The car contains all the hardware necessary to make the wheels turn.  If a forklift lifts the car so that the wheels do not touch the ground and you get in the car, start the engine, and step on the accelerator, the wheels start turning.  The car, however, does not start moving forward.

What is missing? Without frictional forces your car will not accelerate.  If you are parked on an icy surface the wheels will turn, but your car does not accelerate.  The center of mass of a system acted on only by internal forces cannot accelerate.  This is a consequence of Newton's third law.  We need an external force to accelerate the car, and that force is friction.

How does friction accelerate your car?

Assume you want the car to accelerate towards the right.  When a wheel is rolling the contact point is not sliding at all.  When a rolling wheel is accelerating, internal forces try to accelerate the contact point backward.  The force of static friction now is directed towards the right and it cancels those forces.  Fhe force of static friction is the only external force acting on the car in the horizontal direction, and without it there would be no net force to accelerate the car.

This is the same happening when we walk. Between our feet and the pavement there is a static friction.  

Space mining

"With our own planet’s resources under ever-growing pressure and competition, could the mining of asteroids and even other planets provide a more sustainable path for development?  For our latest readers’ Q&A we’ve lined up a panel of experts that includes some of the leading academics looking at the possibilities of extra-terrestrial mining and two of the companies that hope to develop the technology and expertise to make it happen."
http://www.theengineer.co.uk/aerospace/news/the-engineer-qa-space-mining/1015824.article