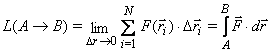1 Gal

Source Wikipedia: "The gal, sometimes called galileo, (symbol Gal) is a unit of acceleration used extensively in the science ofgravimetry. The gal is defined as 1 centimeter per second squared (1 cm/s²). The milligal (mGal) and microgal (µGal) refer respectively to one thousandth and one millionth of a gal. The gal is not part of the International System of Units (SI). However, in 1978 the CIPM decided that it was permissible to use the gal "with the SI until the CIPM considers that [its] use is no longer necessary." The gal is a derived unit, defined in terms of the centimeter-gram-second (CGS) base unit of length, the centimeter, and the second, which is the base unit of time in both the CGS as well as the modern SI system. In SI base units, 1 Gal is precisely equal to 0.01 m/s².The acceleration due to Earth’s gravity (see Standard gravity) at its surface is 976 to 983 Gal, the variation being due mainly to differences in latitude and elevation. Mountains and masses of lesser density within the Earth's crust typically cause variations in gravitational acceleration of tens to hundreds of milligals (mGal). The gravity gradient (variation with height) above Earth's surface is about 3.1 µGal per centimeter of height (3.1×10⁻⁶ s^–2), resulting in a maximum difference of about 2 Gal (0.02 m/s²) from the top of Mount Everest to sea level."

Gravitometer

A gravimeter is an instrument used  for measuring the local gravitational field of the Earth. "A gravimeter is a type of accelerometer, specialized for measuring the constant downward acceleration of gravity, which varies by about 0.5% over the surface of the Earth. Though the essential principle of design is the same as in other accelerometers, gravimeters are typically designed to be much more sensitive in order to measure very tiny fractional changes within the Earth's gravity of 1 g, caused by nearby geologic structures or the shape of the Earth and by temporal tidal variations. This sensitivity means that gravimeters are susceptible to extraneous vibrations including noise that tend to cause oscillatory accelerations. In practice this is counteracted by integral vibration isolation and signal processing. The constraints on temporal resolution are usually less for gravimeters, so that resolution can be increased by processing the output with a longer "time constant". Gravimeters display their measurements in units of gals, instead of ordinary units of acceleration. Gravimeters are used for petroleum and mineral prospecting, seismology, geodesy, geophysical surveys and othergeophysical research, and for metrology." More at http://en.wikipedia.org/wiki/Gravimeter

"The geoid, simply stated, is the shape that the surface of the oceans would take under the influence of gravity alone. All points on that surface have the same scalar potential - there is no difference in potential energy between any two. In that idealized situation, other influences such as winds due to solar heating, and tides have no effect. The surface of the geoid is farther away from the center of the earth where the gravity is weaker, and nearer where it is stronger. The differences in gravity, and hence the scalar potential field, arise from the uneven distribution of the density of matter in the earth.Specifically, the geoid is the equipotential surface that would coincide with the mean ocean surface of the Earth if the oceans and atmosphere were in equilibrium, at rest relative to the rotating Earth,[1] and extended through the continents (such as with very narrow canals). According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but highly irregular surface that corresponds not to the actual surface of the Earth's crust, but to a surface which can only be known through extensive gravitational measurements and calculations. Despite being an important concept for almost two hundred years in the history of geodesy and geophysics, it has only been defined to high precision in recent decades, for instance by works of Petr Vaníček, and others. It is often described as the true physical figure of the Earth,[1] in contrast to the idealized geometrical figure of a reference ellipsoid." More at Wikipedia: http://en.wikipedia.org/wiki/Geoid

AU

Da Wikipedia

The Moon is 0.0026 ± 0.0001 AU from the Earth
Mercury is 0.39 ± 0.09 AU from the Sun
Venus is 0.72 ± 0.01 AU from the Sun
The Earth is 1.00 ± 0.02 AU from the Sun
Mars is 1.52 ± 0.14 AU from the Sun
Ceres is 2.77 ± 0.22 AU from the Sun
Jupiter is 5.20 ± 0.25 AU from the Sun
Saturn is 9.58 ± 0.53 AU from the Sun
Uranus is 19.23 ± 0.85 AU from the Sun
The New Horizons spacecraft is about 22 AU from the Sun (as of 2012), as it makes its way to Pluto for a flyby.
Neptune is 30.10 ± 0.34 AU from the Sun
The Kuiper belt begins at roughly 30 AU [51]
Pluto is 39.3 ± 9.6 AU from the Sun
Beginning of the scattered disk at 45 AU (10 AU overlap with Kuiper Belt)
Ending of Kuiper belt at 50-55 AU
Eris is 68.01 ± 29.64 AU from the Sun
90377 Sedna is currently (as of 2012) about 87 AU from the Sun
94 AU: termination shock between solar winds/interstellar winds/interstellar medium
96.7 AU: the distance of dwarf planet Eris from the Sun, as of 2009. Eris and its moon are currently the most distant known objects in the Solar System apart from long-period comets and space probes.
100 AU: heliosheath
122 AU: as of September 2012, Voyager 1 is the furthest human-made object from the Sun; it is currently traveling at about 3½ AU/yr.
100-1000 AU: mostly populated by objects from the scattered disc
1000-3000 AU: beginning of Hills cloud/inner Oort cloud
20,000 AU: ending of Hills cloud/inner Oort cloud, beginning of outer Oort cloud
50,000 AU: possible closest estimate of the outer Oort cloud limits (0.8 ly)
100,000 AU: possible farthest estimate of the outer Oort cloud limits (1.6 ly)
230,000 AU: maximum extent of influence of the Sun's gravitational field (Hill/Roche sphere)—beyond this is true interstellar medium. This distance is 1.1 parsecs (3.6 light-years).
Proxima Centauri (the nearest star to Earth, excluding the Sun) is ~268 000 AU from the Sun

Lavoro e teorema energia cinetica

Prima di discutere il lavoro come integrale lungo una linea del prodotto scalare di forza e spostamento infinitesimo, discutiamo un semplice problema unidimensionale che ci può mostrare in modo semplice il legame del lavoro con l'energia cinetica. Prendiamo una particella di massa m a cui sia applicata una forza F, costante in modulo direzione e verso. Sia x l'asse coincidente con la direzione della forza  su cui si muove, di conseguenza, la particella di massa m. Siccome la forza è costante anche l'accelerazione lo sarà:  

Abbiamo quindi visto con questo semplice calcolo unidimensionale che esiste una relazione tra la quantità  dimensionata come [forza∙spotamento] con la differenza di due grandezze che sono dimensionate [massa.velocità^2]. Siccome [forza]=[massa∙accelerazione]=[massa∙velocità/tempo], abbiamo che  [forza∙spostamento]=[massa∙(velocità/tempo)∙spostamento]=[msssa∙velocità∙spotamento/tempo]=[m∙velocità^2].

         

Se definiamo E_cin=1/2 mv² come l' energia cinetica allora l'equazione ci dice che la variazione dell'energia cinetica ΔE_cin=1/2 mv² − 1/2 mv_o² ossia la differenza tra l'energia cinetica finale e quella iniziale è uguale al prodotto di F∙per (x-x_o) che è il  lavoro compiuto dalla forza applicata alla particella. L'unità di misura del lavoro nel sistema internazionale è il  Joule ed è definito come il lavoro compiuto dalla forza di un Newton che agisce per un metro. Passiamo adesso ad affrontare la definizione di lavoro per uno spostamento generico.

Definiamo lavoro L compiuto da una forza F su una particella che subisce uno spostamento Δr come:

L=F∙Δr = F Δr cos(F,Δr)

                                                                   

 In genere F varia durante lo spostamento: a ogni piccolo spostamento i-esimo Δr_i lungo la traiettoria della massa corrisponderà una forza diversa F(r_i). Il lavoro totale sarà la somma di tutti i singoli lavori  L_i  per gli spostamenti Δr_i :

 dove N è il numero totale di spostamenti  da A a B. Il calcolo del lavoro sarà tanto più preciso quanto più piccoli sono gli intervalli. Per Δr →0 si avrà: 

L(A→B) è il lavoro fatto dalla forza quando la massa passa da A a B lungo il percorso dato. Il lavoro è definito come l’integrale lungo il percorso nello spazio da A a B del prodotto scalare della forza per lo spstamento infinitesimo.

Generalizziamo ora la relazione trovata nel caso unidimensionale.

Scomponiamo la forza F come somma di due vettori componenti F_parall  e F_perp che sono rispettivamente parallelo e perpendicolare allo spostamento:

(solo la componente della forza parallela allo spostamento lavora). La velocità v che compare nelle formule sritte sopra è la velocità scalare lungo la curva.
Dal calcolo vediamo che: Il lavoro compiuto dalla forza F produce una variazione dell'energia cinetica della particella. Con “variazione” dell’energia cinetica si intende l’energia cinetica finale meno quella iniziale.

Velocità areale

Relazione tra momento angolare e velocità areale.

Per la discussione utilizziamo il momento angolare descritto con le componenti polari della velocità. Possiamo infatti scomporre il vettore velocità in due componenti, come in figura seguente:

La componente della velocità diretta come direzioni u_r è detta “radiale”, quella diretta come u_θ è detta “trasversa” . Per quanto riguarda i moduli delle due componenti si ha che v_r=dr/dt, che indica la variazione della distanza radiale nel tempo, e v_θ= r dθ/dt che indica una rivoluzione sulla circonferenza di raggio r a una velocità angolare data da dθ/dt.

Quindi:

Calcoliamo ora il momento angolare rispetto al  polo del riferimento polare. Si ha che:

Il vettore momento della quantità di moto è perpendicolare al piano che contiene il raggio vettore e il vettore velocità. La direzione di questo vettore è data da quella del vettore unitari u_z. Notiamo che, utilizzando le componenti polari della velocità, nell’espressione finale compare solo la componente trasversale della velocità, che contiene una velocità angolare.

Immaginiamo ora di considerare l’area spazzata dal raggio vettore durante il moto lungo del punto lungo la traiettoria. Consideriamo il caso in cui la traiettoria giaccia sempre su di un piano. La curva crea una regione con una certa area nel piano della figura, regione compresa tra la curva, l’asse del riferimento polare e il raggio vettore OP.

Se la particella si muove, in un certo tempo dt il punto si muove da P a P’. L’area cresce di una quantità dArea, come in figura. Se dt è piccolo, l’arco si confonde con la corda ed è circa uguale all’altezza del triangolo OPP’. L’area di questo triangolo è:

dArea= ½ r²dθ

Dividiamo per il tempo ed abbiamo la velocità areolare: dArea/dt= = ½ r²dθ/dt.

Consideriamo ora un caso molto interessante. Supponiamo che la particella si muova soggetta a una forza centrale con centro nel polo O. Se calcoliamo il momento angolare rispetto allo stesso polo, sappiamo che esso deve essere costante in quanto il momento della forza centrale è nullo. Questo significa che la particella in moto dovrà muoversi mantenendo L costante. Come conseguenza il piano dell’orbita (che contiene raggio vettore e velocità) deve rimaner costante.

Il modulo è inoltre legato alla velocità areale. Si ha:

In un campo centrale, la velocità areolare è costante poiché lo è il momento angolare.

Il campo gravitazionale è un campo centrale. Vale la seconda legge di Keplero afferma che il raggio vettore che unisce il centro del Sole con il centro del pianeta descrive aree uguali in tempi uguali. La conseguenza di questa legge è che la velocità orbitale non è costante, ma varia lungo l'orbita. In prossimità del perielio, dove il raggio vettore è più corto che all'afelio, il pianeta è più veloce. Ne segue quindi che la velocità orbitale è massima al perielio e minima all'afelio.

Domanda di teoria - conservazione energia

Discutere la conservazione dell'energia

Ci sono delle grandezze fisiche che sono delle costanti del moto. Una costante del moto è una grandezza che resta invariata durante l'evoluzione del sistema. Abbiamo visto per esempio il momento angolare, che, nel caso del campo gravitazionale e se calcolato rispetto al centro del campo, rimane costante.  Così, nell'orbita dei pianeti, se il pianeta è vicino al sole esso si muove più veloce, e se è lontano, si muove più lento. Il prodotto vettoriale del raggio vettore e della velocità resta però costante.

Le costanti del moto sono quindi degli oggetti che sono conservati durante l'evoluzione nel tempo del sistema. Cercare quindi le costanti del moto ci porta a stabilire delle leggi di conservazione. Oltre a quella riguardante il momento angolare, esiste la conservazione dell'energia. L'energia in meccanica coinvolge i concetti di energia cinetica, energia potenziale e lavoro. 

Vediamo che forma ha l'energia quando diventa una costante del moto. Consideriamo  una forza che lavora su una particella che si muove tra due punti dello spazio. Supponiamo che il lavoro non dipenda dal percorso fatto tra i due punti. Immaginiamo quindi che la forza provenga da un campo definito in una certa regione dello spazio e che, scelta la coppia di punti iniziale A e finale B  facendo un percorso qualsiasi da A a B, si ottenga sempre lo stesso lavoro.  

Prendiamo A, B ed il riferimento O come in figura. :

L’espressione è valida per l’additività del lavoro come integrale. Poiché il lavoro non dipende dal percorso, il lavoro L(O->B) sarà una funzione W solo del punto iniziale O e del punto finale B; lo stesso vale per L(O->A), che è una funzione W del punto O e del punto B. Il lavoro L(A->B) è quindi la differenza della funzione  W, valutata una volta come W(O,B) e un'altra volta come funzione W(O,A).  Si definisce l’energia potenziale U(O,A) come –W(O,A) e U(O,B) come –W(O,B).
Ricordiamo inoltre che vale il teorema dell’energia cinetica. Quindi:

La somma dell’energia cinetica e dell’energia potenziale è l’energia meccanica totale, che è una costante del moto se la forza un lavoro che non dipende del percorso fatto ma solo dai punti iniziale e finale. Siccome la costante del moto "energia" resta costante al variare del tempo, si dice che l'energia è conservata. 
La forza che genera una dinamica con l'energia costante è una forza conservativa.

Notiamo anche che l’energia potenziale è data a meno di una costante. Supponiamo di avere oltre al punto O un altro punto O’.

L’energia potenziale è data a meno della costante U(O’,O) che non ha influenza nel calcolo della differenza di energia potenziale.

Riferimenti inerziali e non

In fisica, un sistema inerziale (anche sistema di riferimento inerziale o sistema di riferimento galileiano) è un riferimento in cui si vede verificato il primo principio della dinamica (principio di inerzia). In questo sistema viene verificata la Seconda Legge di Newton, senza la nacessità di introdurre delle forze fittizie per giustificare il moto delle masse. Inoltre, tutti i sistemi inerziali sono in uno stato di moto rettilineo l'uno rispetto all'altro, non stanno quindi accelerando l'uno rispetto all'altro. Un sistema di riferimento non inerziale è un sistema accelerato rispetto ad uno inerziale. Con questo si intende che il riferimento non inerziale è un sistema che accelera o ruota, o entrambe le cose, rispetto a quello inerziale.
Le misure fatte in un sistema inerziale possono essere convertite nelle misure fatte in un altro riferimento inerziale da una semplice trasformazione (le trasformazioni di Galileo nella fisica newtoniana e le trasformazioni di Lorentz nella relatività speciale). Le leggi fisiche hanno la stessa forma in tutti i sistemi inerziali. In un riferimento non inerziale, le leggi della fisica dipendono dall'accelerazione di tale riferimento, e quindi le forze fisiche devono essere integrate da forze fittizie. In sintesi, in un sistema di riferimento inerziale, le leggi della meccanica prenderanno il loro aspetto più semplice.
In un sistema inerziale, la prima legge di Newton (la legge di inerzia), è soddisfatta: Qualsiasi movimento libero ha una velocità costante in modulo e direzione. La seconda legge di Newton per una particella assume la forma:

F = m a

con F la forza risultante (un vettore), m la massa di una particella e a accelerazione della particella (un vettore), che sarebbe misurata da un osservatore a riposo nel riferimento. La forza F è la somma vettoriale di tutte le "reali" forze sulla particella (elettromagnetica, gravitazionale, nucleare e così via). Al contrario, la seconda legge di Newton in un sistema di riferimento accelerato, assume sempre la forma:

F'= m a’

che ha lo stesso aspetto come quella che si ha in un sistema inerziale, ma ora la forza F' non è solo la risultante di F, perché essa contiene ulteriori componenti.  Ad esempio, in un riferimento che ruota a velocità angolare Ω costante attorno ad un asse fisso, si ha:

F'= F −  2m Ω x v'−m Ω x (Ω x r')

dove la rotazione del riferimento è espressa dal vettore Ω, che indica la direzione dell'asse di rotazione, con una grandezza pari all'incremento dell'angolo di rotazione. Il  simbolo x indica il prodotto vettoriale tra due vettori. Il vettore r' individua la posizione del corpo e vettore v' è la velocità del corpo secondo un osservatore rotante (diversa dalla velocità v vista da un osservatore inerziale). I termini in più in F' sono  "fittizi" (il primo termine supplementare è la forza di Coriolis, la seconda la forza centrifuga).Questi termini hanno la seguente proprietà: svaniscono quando Ω = 0, cioè, sono pari a zero per un sistema inerziale (il che, ovviamente, non ruota).

Tutti gli osservatori concordano sulle forze reali, F; solo gli osservatori non inerziali hanno bisogno di forze fittizie. Le leggi della fisica nel sistema inerziale sono più semplici perché le forze fittizie non sono presenti.

Al tempo di Newton, le stelle fisse erano state scelte come riferimento inerziale, dato che si presumevano in quiete rispetto allo spazio assoluto. In riferimenti che erano a riposo rispetto alle stelle fisse o in traslazione uniforme rispetto a queste stelle, valevano le leggi di Newton del moto. Al contrario, in riferimenti accelerati rispetto alle stelle fisse,  le leggi del moto non hanno la loro forma più semplice, ma devono essere integrate con l'aggiunta di forze fittizie. Ai giorni nostri il concetto di sistemi inerziali di riferimento non è più legato a uno delle stelle fisse o allo spazio assoluto. Piuttosto, l'identificazione di un sistema inerziale si basa sulla semplicità delle leggi della fisica. In particolare, l'assenza di forze fittizie è la loro proprietà di identificazione.

Discutiamo ora le trasformazioni da un sistema ad un altro, secondo Galileo.

Prendiamo un sistema fisso xyz ed uno mobile x’y’z'. Ricordiamo che i vettori posizione soddisfano la regola della somma vettoriale. Derivando la somma rispetto al tempo otteniamo che la velocità v di un punto P osservata nel sistema fisso xyz è uguale alla somma della velocità v’ osservata in x’y’z' più la velocità V del riferimento x'yz''.

.v=v’+V (*)

Supponiamo che V sia costante: se deriviamo rispetto al tempo le velocità vediamo che

a=a’

Vediamo quindi la stessa accelerazione in xyz ed in x’yz'’. Quindi per la legge di Newton:

F=ma=ma’

Adesso immaginiamo che x’yz'’ si muova accelerando con una accelerazione A rispetto ad xyz. Derivando la (*) si ha:

 a=a’+A

E quindi la legge di Newton diventa, F=ma=ma’+mA, F−mA=ma’

Facciamo un esempio. Un oggetto viene lasciato cadere all’interno di un vagone che si muove accelerando.

Un osservato fermo vicino alla strada ferrata, vede l’oggetto cadere secondo la verticale sotto l’effetto della gravità. Un osservatore sul vagone invece lo vede cadere verso la parte posteriore del vagone. Egli pensa che sull’oogetto agiscono due forze: la gravità ed una “attrazione” da parte della parete di fondo.

Ecco che per l’osservatore sul sistema accelerato compare la forza fittizia F(fittizia)=-mA.

Se abbiamo una massa vincolata al soffitto del vagone con una fune, all’osservatore sul vagone che accelera, la fune appare avere un’inclinazione rispetto alla verticale.

L’osservatore pensa che la massa sia in equilibrio sotto l’effetto della gravità, della tensione del filo e dell’attrazione della parete di fondo. Un osservatore fisso rispetto alla strada ferrata vede invece il filo inclinato perché la tensione della fune deve avere una componente orizzontale, tale da dare alla massa m un’accelerazione orizzontale pari ad A.

Domanda di teoria - Momento angolare in coordinate polari

Discutere il momento della quantità di moto in coordinate polari.

Prima di discutere il momento del vettore “quantità di moto”, ricordiamo che le coordinate polari di un punto nel piano sono basate sulla distanza r da un polo fisso, data dal modulo del raggio vettore che unisce il polo al punto P e sull’angolo tra la direzione del raggio vettore e l’asse di riferimento (ad esempio x in figura) 

Il legame delle coordinate cartesiane con le coordinate polari è dato da x=r cosθ, y=r sinθ.
Consideriamo ora una traiettoria e un punto su di essa P. A P, la velocità è tangenziale la traiettoria. Prendiamo ora il riferimento polare e disegniamo la direzione radiale (u_r) e la direzione a essa perpendicolare (u_θ). In genere, il vettore velocità ha una direzione diversa dalle due direzioni u_r u_θ.

Possiamo pensare di scomporre il vettore velocità in due componenti, come in figura seguente:

La componente della velocità diretta come direzioni u_r è detta “radiale”, quella diretta come u_θ è detta “trasversa” o trasversale. Per quanto riguarda i moduli delle due componenti si ha che v_r=dr/dt, che indica la variazione della distanza radiale nel tempo, e v_θ= r dθ/dt che indica una rivoluzione sulla circonferenza di raggio r a una velocità angolare data da dθ/dt.

Quindi:

Calcoliamo ora il momento di questa velocità rispetto al polo del riferimento polare:

 Il primo prodotto è nullo perché prodotto esterno di vettori paralleli. Vediamo quindi che rimane solo il termine che contiene la velocità trasversale. Moltiplichiamo per la massa per avere il momento della quantità di moto:

Il vettore momento della quantità di moto è perpendicolare al piano che contiene il raggio vettore e il vettore velocità. La direzione di questo vettore è data da quella del vettore unitari u_z. Notiamo che, utilizzando le componenti polari della velocità, nell’espressione finale compare solo la componente trasversale della velocità, che contiene una velocità angolare. Ciò giustifica il fatto che il momento della quantità di moto venga detto “momento angolare” Siccome raggio vettore e direzione trasversa sono perpendicolari, il modulo è semplice da calcolare.

Treasure Map

Long John Silver, a pirate, has buried his treasure on an island with five trees located at the following points: A (30.0 m, –20.0 m), B (60.0 m, 80.0 m), C (–10.0 m, –10.0 m), D (40.0 m, –30.0 m), and E (–70.0 m, 60.0 m). All of the points are measured relative to some origin, as in Figure. Long John’s map instructs you to start at A and move toward B, but cover only 1/2 the distance between A and B. Then move toward C, covering 1/3 the distance between your current location and C. Then move toward D, covering 1/4 the distance between where you are and D. Finally, move toward E, covering 1/5 the distance between you and E, stop, and dig.

A (30.0 m, –20.0 m), B (60.0 m, 80.0 m), C (–10.0 m, –10.0 m)

D (40.0 m, –30.0 m), and E (–70.0 m, 60.0 m).

The intermediate points are F,G,H and I. For each of coordinates x and y:
 F = A + 1/2 (B - A)
 G = F + 1/3 (C - F)
 H= G + 1/4 (D - G)
 I = H + 1/5 (E - H)

Vectors:
F = (30,-20) + 1/2 ((60,80) - (30,-20)) = (30,-20) + 1/2 (30,100) =  (45, 30)

 G = (45,30) + 1/3 ((-10,-10) - (45, 30)) = (45, 30) + 1/3 (-55, -40) = = (45-55/3,30-40/3)
 

H= ... 

or you can use a program

XA=30.0

YA=-20.0

XB=60.0

YB=80.0

XC=-10.0

YC=-10.0

XD=40.0

YD=-30.0

XE=-70.0

YE=60.0

XF=XA+(XB-XA)/2.

YF=YA+(YB-YA)/2.

XG=XF+(XC-XF)/3.

YG=YF+(YC-YF)/3.

XH=XG+(XD-XG)/4.

YH=YG+(YD-YG)/4.

XI=XH+(XE-XH)/5.

YI=YH+(YE-YH)/5.

print *,XI,YI

output: 10. 16.

Treasure Island is an adventure novel by author Robert Louis Stevenson, narrating a tale of "buccaneers and buried gold". Traditionally considered a coming of age story, it is an adventure tale known for its superb atmosphere, character and action, and also a wry commentary on the ambiguity of morality—as seen in Long John Silver—unusual for children's literature then and now. The influence of Treasure Island on popular perception of pirates is vast, including treasure maps with an 'X', schooners, the Black Spot, tropical islands, and one-legged seamen with parrots on their shoulders.

Velocità e accelerazione in coordinate polari

Velocità e accelerazione in coordinate polari.

  

Abbiamo discusso la velocità e l’accelerazione secondo le coordinate cartesiane ed anche intrinsecamente alla traiettoria. Ora discutiamo come si scrivono utilizzando un riferimento polari.

Immaginiamo di avere una particella che si muove su una certa traiettoria. Noi sappiamo che la sua velocità, come vettore, deve essere tangente la traiettoria. Passiamo ora a scomporre questa velocità secondo due direzioni, che sono quella radiale, ossia del raggio vettore che va dal polo O alla posizione P della particella, e quella trasversa, che corrisponde all’incremento dell’azimut, l’angolo che c’è la direzione radiale e l’asse di riferimento OX. Notiamo che queste direzioni NON sono legate alle direzioni intrinseche alla traiettoria (tangente e centripeta). La direzione radiale e quella trasversa sono tra di loro perpendicolari.

Dato che le due direzioni, radiale e trasversa, sono perpendicolari l’una all’altra, abbiamo che la velocità ha due componenti: quella radiale e quella trasversa. Ossia la velocità della particella è un vettore somma di due vettori componenti come nella figura seguente:

 Dimostriamo che:

Indichiamo in una figura le direzioni del vettori unitari e scriviamo come si può esprimere il raggio vettore da O a P secondo. Esso è il prodotto del modulo r, distanza di P da O, e del suo vettore unitario (versore).

 Deriviamo il raggio vettore secondo il tempo.

Che è ciò che volevamo dimostrare. Abbiamo utilizzato la derivata del versore radiale. Ricordiamoci che la derivata di un vettore che ha  modulo costante è sempre un vettore perpendicolare al vettore da derivare. La derivata del versore radiale è quindi pari al versore trasverso, moltiplicato per la derivata dellìangolo rispetto al tempo. Quanto vale la derivata del versore trasversale? Vediamolo nella seguente figura.

La derivata del versore trasverso deve essere un vettore a esso perpendicolare. E' quindi il versore radiale, cambiato di segno, moltiplicato per la derivata dell'angolo rispetto al tempo.
Utilizzando questo risultato, svolgiamo i calcoli:

Quindi abbiamo che: 

Oscillatore smorzato

Un oscillatore armonico è un sistema che, se spostato dalla sua posizione di equilibrio, sperimenta una forza di richiamo F proporzionale allo spostamento x secondo la legge di Hooke: F=−kx dove k è una costante positiva. Se F è l'unica forza che agisce sul sistema, il sistema è detto oscillatore armonico semplice, ed è sottoposto al moto armonico semplice: oscillazioni sinusoidali attorno al punto di equilibrio, con un’ampiezza costante e una frequenza costante (che non dipende dall'ampiezza). Se una forza di attrito (smorzamento) proporzionale alla velocità è anche presente, l'oscillatore armonico è descritto come un oscillatore smorzato. In tale situazione, la frequenza delle oscillazioni è più piccola rispetto al caso non smorzato, e l'ampiezza delle oscillazioni diminuisce con il tempo. Se una forza esterna dipendente dal tempo è presente, l'oscillatore armonico è descritto come un oscillatore forzato. L'oscillatore armonico semplice non ha alcuna forza motrice e nessun attrito (smorzamento), quindi la forza netta è solo F=−kx. Usando la seconda legge di Newton: F=ma, otteniamo:

Definiamo ω_o² =k/m, l’equazione si scrive allora:

La soluzione generale è: x=Acos(ω_ot+ф), dove l’ampiezza è A e la fase iniziale ф, che soddisfano le condizione iniziali. Un oscillatore armonico forzato è dato dall'equazione: 

.dove  A₀ è l’ampiezza della forzante ed ω_f  è la pulsazione della forzante.

Lo smorzamento può essere visto come una forza sincrona alla velocità ma opposta in verso. Per smorzamento si può quindi assumere la forza F legata a v da F=−cv dove c è il coefficiente di attrito viscoso, dato in newton-secondo/metro.

 

Nell’oscillatore smorzato la massa è attaccata ad una molla e ad uno smorzatore (damper). Nell’equazione seguente, il coefficiente di smorzamento è rappresentato da b.

Un oscillatore armonico smorzato soddisfa l’equazione:

 

 dove b è determinato sperimentalmente dalla relazione  F = − bv. Un esempio è un oscillatore posto sott’acqua, se si suppone che la forza esercitata dall’acqua sia lineare in v.  La pulsazione dell’oscillatore smorzato è: 

 dove Ξ=b/2m. La pulsazione data dalla radice quadrata si dice pulsazione ridotta.

Per trovare questo risultato applichiamo il metodo di soluzione dell’equazione tramite i numeri complessi. Proponiamo che la soluzione sia:

Sostituisco nell’eq(*):

Per essere soddisfatta l’equazione, il numero complesso in parentesi quadra deve essere nullo. Devono essere nulle quindi la parte reale e la parte immaginaria.

.da cui si ricava che il coefficiente di smorzamento dell ampiezza e: μ=b/(2m).

Inoltre

da cui la pulsazione ridotta data sopra.

Notiamo che quest'ultima equazione può dar luogo a pulsazioni reali oppure a pulsazioni immaginarie. Nel caso che   ω_o  è maggiore di b/2m, allora    ω è reale e la soluzione è un'oscillazione smorzata. Se invece   ω_o  è minore o uguale a b/2m, allora    ω è complessa e pari a   ω =i q; la soluzione è un esponente decrescente e si dice che il moto e "sovrasmorzato".